| Date | November 2013 | Marks available | 11 | Reference code | 13N.3dm.hl.TZ0.2 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Draw, Find, Show that, and Write down | Question number | 2 | Adapted from | N/A |
Question
The following figure shows the floor plan of a museum.
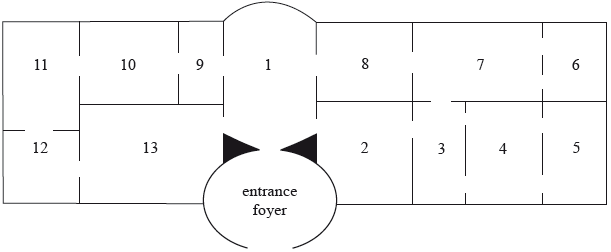
(a) (i) Draw a graph G that represents the plan of the museum where each exhibition room is represented by a vertex labelled with the exhibition room number and each door between exhibition rooms is represented by an edge. Do not consider the entrance foyer as a museum exhibition room.
(ii) Write down the degrees of the vertices that represent each exhibition room.
(iii) Virginia enters the museum through the entrance foyer. Use your answers to (i) and (ii) to justify why it is possible for her to visit the thirteen exhibition rooms going through each internal doorway exactly once.
(b) Let G and H be two graphs whose adjacency matrices are represented below.
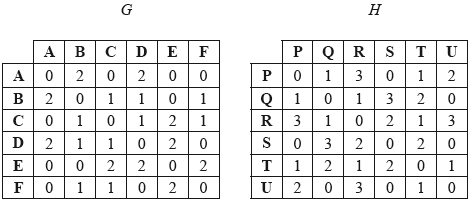
Using the adjacency matrices,
(i) find the number of edges of each graph;
(ii) show that exactly one of the graphs has a Eulerian trail;
(iii) show that neither of the graphs has a Eulerian circuit.
Markscheme
(a) (i) 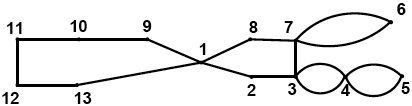 (M1)A1
(M1)A1
Note: Do not penalize candidates who include the entrance foyer.
(ii) the degrees of the vertices are 4, 2, 4, 4, 2, 2, 4, 2, 2, 2, 2, 2, 2 A1
(iii) the degree of all vertices is even and hence a Eulerian circuit exists, A1
hence it is possible to enter the museum through the foyer and visit each room 1–13 going through each internal doorway exactly once AG
Note: The connected graph condition is not required.
[4 marks]
(b) (i) 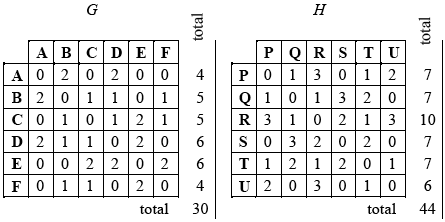 (M1)
(M1)
graph G has 15 edges and graph H has 22 edges A1A1
(ii) the degree of every vertex is equal to the sum of the numbers in the corresponding row (or column) of the adjacency table
exactly two of the vertices of G have an odd degree (B and C) A1
H has four vertices with odd degree A1
G is the graph that has a Eulerian trail (and H does not) R1
(iii) neither graph has all vertices of even degree R1
therefore neither of them has a Eulerian circuit AG
[7 marks]
Examiners report
Part (a) was generally well answered. There were many examples of full marks in this part. Part (b) caused a few more difficulties, although there were many good solutions. Few candidates used the matrix to find the number of edges, preferring instead to draw the graph. A surprising number of students confused the ideas of having vertices of odd degree.

