| Date | May 2014 | Marks available | 2 | Reference code | 14M.3dm.hl.TZ0.1 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Draw | Question number | 1 | Adapted from | N/A |
Question
The weighted graph K, representing the travelling costs between five customers, has the following adjacency table.
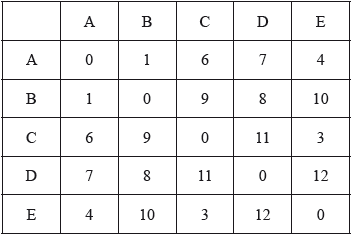
Draw the graph \(K\).
Starting from customer D, use the nearest-neighbour algorithm, to determine an upper bound to the travelling salesman problem for K.
By removing customer A, use the method of vertex deletion, to determine a lower bound to the travelling salesman problem for K.
Markscheme
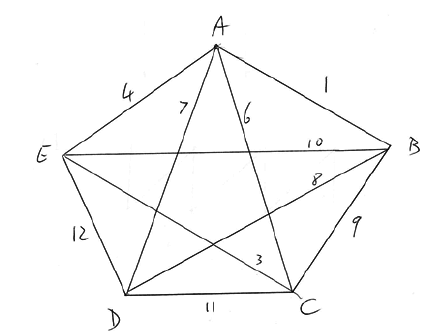
complete graph on five vertices A1
weights correctly marked on graph A1
[2 marks]
clear indication that the nearest-neighbour algorithm has been applied M1
DA (or 7) A1
AB (or 1) BC (or 9) A1
CE (or 3), ED (or 12), giving UB = 32 A1
[4 marks]
attempt to use the vertex deletion method M1
minimum spanning tree is ECBD A1
(EC 3, BD 8, BC 9 total 20)
reconnect A with the two edges of least weight, namely AB (1) and AE (4) M1
lower bound is 25 A1
[4 marks]

