| Date | May 2014 | Marks available | 10 | Reference code | 14M.3dm.hl.TZ0.3 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Draw and Prove that | Question number | 3 | Adapted from | N/A |
Question
(a) Draw a spanning tree for
(i) the complete graph, \({K_4}\);
(ii) the complete bipartite graph, \({K_{4,4}}\).
(b) Prove that a simple connected graph with n vertices, where \(n > 1\), must have two vertices
of the same degree.
(c) Prove that every simple connected graph has at least one spanning tree.
Markscheme
(a) (i)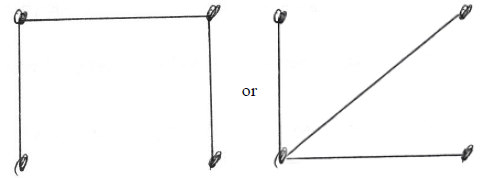 A1
A1
Note: Or equivalent not worrying about the orientation.
(ii)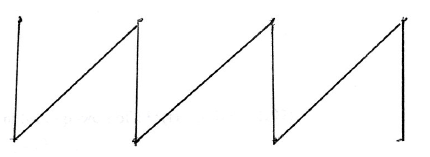 A1
A1
Note: Other trees are possible, but must clearly come from the bipartite graph, so, for example, a straight line graph is not acceptable unless the bipartite nature is clearly shown eg, with black and white vertices.
[2 marks]
(b) graph is simple implies maximum degree is \(n - 1\) A1
graph is connected implies minimum degree is 1 A1
by a pigeon-hole principle two vertices must have the same degree R1
[3 marks]
(c) if the graph is not a tree it contains a cycle A1
remove one edge of this cycle M1
the graph remains connected A1
repeat until there are no cycles M1
the final graph is connected and has no cycles A1
so is a tree AG
Note: Allow other methods eg, induction, reference to Kruskal’s algorithm.
[5 marks]
Total [10 marks]

