| Date | May 2015 | Marks available | 3 | Reference code | 15M.2.hl.TZ2.9 |
| Level | HL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 9 | Adapted from | N/A |
Question
Natasha lives in Chicago and has relatives in Nashville and St. Louis.
Each time she visits her relatives, she either flies or drives.
When travelling to Nashville, the probability that she drives is \(\frac{4}{5}\), and when travelling to St. Louis, the probability that she flies is \(\frac{1}{3}\).
Given that the probability that she drives when visiting her relatives is \(\frac{13}{18}\), find the probability that for a particular trip,
she travels to Nashville;
she is on her way to Nashville, given that she is flying.
Markscheme
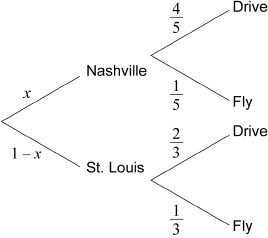
attempt to set up the problem using a tree diagram and/or an equation, with the unknown \(x\) M1
\(\frac{4}{5}x + \frac{2}{3}(1 - x) = \frac{{13}}{{18}}\) A1
\(\frac{{4x}}{5} - \frac{{2x}}{3} = \frac{{13}}{{18}} - \frac{2}{3}\)
\(\frac{{2x}}{{15}} = \frac{1}{{18}}\)
\(x = \frac{5}{{12}}\) A1
[3 marks]
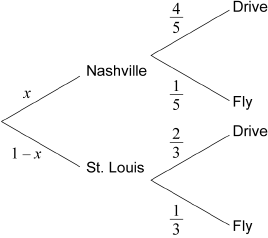
attempt to set up the problem using conditional probability M1
EITHER
\(\frac{{\frac{5}{{12}} \times \frac{1}{5}}}{{1 - \frac{{13}}{{18}}}}\) A1
OR
\(\frac{{\frac{5}{{12}} \times \frac{1}{5}}}{{\frac{1}{{12}} + \frac{7}{{36}}}}\) A1
THEN
\( = \frac{3}{{10}}\) A1
[3 marks]
Total [6 marks]

