| Date | November 2015 | Marks available | 6 | Reference code | 15N.2.hl.TZ0.6 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 6 | Adapted from | N/A |
Question
Josie has three ways of getting to school. \(30\% \) of the time she travels by car, \(20\% \) of the time she rides her bicycle and \(50\% \) of the time she walks.
When travelling by car, Josie is late \(5\% \) of the time. When riding her bicycle she is late \(10\% \) of the time. When walking she is late \(25\% \) of the time. Given that she was on time, find the probability that she rides her bicycle.
Markscheme
EITHER
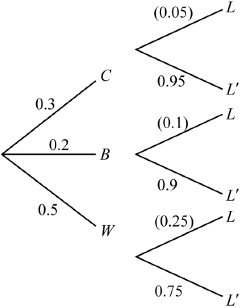 M1A1A1
M1A1A1
Note: Award M1 for a two-level tree diagram, A1 for correct first level probabilities, and A1 for correct second level probabilities.
OR
\({\text{P}}(B|L') = \frac{{{\text{P}}(L'|B){\text{P}}(B)}}{{{\text{P}}(L'|B){\text{P}}(B) + {\text{P}}(L'|C){\text{P}}(C) + {\text{P}}(L'|W){\text{P}}(Q)}}\;\;\;\left( { = \frac{{{\text{P}}(B \cap L'}}{{{\text{P}}(L')}}} \right)\) (M1)(A1)(A1)
THEN
\({\text{P}}(B|L') = \frac{{0.9 \times 0.2}}{{0.9 \times 0.2 + 0.95 \times 0.3 + 0.75 \times 0.5}}\;\;\;\left( { = \frac{{0.18}}{{0.84}}} \right)\) M1A1
\( = 0.214\;\;\;\left( { = \frac{3}{{14}}} \right)\) A1
[6 marks]

