| Date | November 2014 | Marks available | 3 | Reference code | 14N.2.hl.TZ0.13 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Show that | Question number | 13 | Adapted from | N/A |
Question
The vertical cross-section of a container is shown in the following diagram.
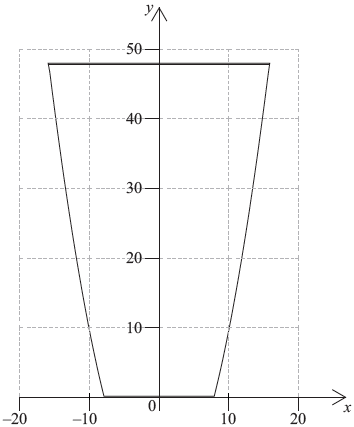
The curved sides of the cross-section are given by the equation \(y = 0.25{x^2} - 16\). The horizontal cross-sections are circular. The depth of the container is \(48\) cm.
If the container is filled with water to a depth of \(h\,{\text{cm}}\), show that the volume, \(V\,{\text{c}}{{\text{m}}^3}\), of the water is given by \(V = 4\pi \left( {\frac{{{h^2}}}{2} + 16h} \right)\).
The container, initially full of water, begins leaking from a small hole at a rate given by \(\frac{{{\text{d}}V}}{{{\text{d}}t}} = - \frac{{250\sqrt h }}{{\pi(h + 16)}}\) where \(t\) is measured in seconds.
(i) Show that \(\frac{{{\text{d}}h}}{{{\text{d}}t}} = - \frac{{250\sqrt h }}{{4{\pi ^2}{{(h + 16)}^2}}}\).
(ii) State \(\frac{{{\text{d}}t}}{{{\text{d}}h}}\) and hence show that \(t = \frac{{ - 4{\pi ^2}}}{{250}}\int {\left( {{h^{\frac{3}{2}}} + 32{h^{\frac{1}{2}}} + 256{h^{ - \frac{1}{2}}}} \right){\text{d}}h} \).
(iii) Find, correct to the nearest minute, the time taken for the container to become empty. (\(60\) seconds = 1 minute)
Once empty, water is pumped back into the container at a rate of \(8.5\;{\text{c}}{{\text{m}}^3}{{\text{s}}^{ - 1}}\). At the same time, water continues leaking from the container at a rate of \(\frac{{250\sqrt h }}{{\pi (h + 16)}}{\text{c}}{{\text{m}}^3}{{\text{s}}^{ - 1}}\).
Using an appropriate sketch graph, determine the depth at which the water ultimately stabilizes in the container.
Markscheme
attempting to use \(V = \pi \int_a^b {{x^2}{\text{d}}y} \) (M1)
attempting to express \({x^2}\) in terms of \(y\) ie \({x^2} = 4(y + 16)\) (M1)
for \(y = h,{\text{ }}V = 4\pi \int_0^h {y + 16{\text{d}}y} \) A1
\(V = 4\pi \left( {\frac{{{h^2}}}{2} + 16h} \right)\) AG
[3 marks]
(i) METHOD 1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{{{\text{d}}h}}{{{\text{d}}V}} \times \frac{{{\text{d}}V}}{{{\text{d}}t}}\) (M1)
\(\frac{{{\text{d}}V}}{{{\text{d}}h}} = 4\pi (h + 16)\) (A1)
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{1}{{4\pi (h + 16)}} \times \frac{{ - 250\sqrt h }}{{\pi (h + 16)}}\) M1A1
Note: Award M1 for substitution into \(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{{{\text{d}}h}}{{{\text{d}}V}} \times \frac{{{\text{d}}V}}{{{\text{d}}t}}\).
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{{250\sqrt h }}{{4{\pi ^2}{{(h + 16)}^2}}}\) AG
METHOD 2
\(\frac{{{\text{d}}V}}{{{\text{d}}t}} = 4\pi (h + 16)\frac{{{\text{d}}h}}{{{\text{d}}t}}\;\;\;\)(implicit differentiation)(M1)
\(\frac{{ - 250\sqrt h }}{{\pi (h + 16)}} = 4\pi (h + 16)\frac{{{\text{d}}h}}{{{\text{d}}t}}\;\;\;\)(or equivalent) A1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{1}{{4\pi (h + 16)}} \times \frac{{ - 250\sqrt h }}{{\pi (h + 16)}}\) M1A1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{{250\sqrt h }}{{4{\pi ^2}{{(h + 16)}^2}}}\) AG
(ii) \(\frac{{{\text{d}}t}}{{{\text{d}}h}} = - \frac{{4{\pi ^2}{{(h + 16)}^2}}}{{250\sqrt h }}\) A1
\(t = \int { - \frac{{4{\pi ^2}{{(h + 16)}^2}}}{{250\sqrt h }}} {\text{d}}h\) (M1)
\(t = \int { - \frac{{4{\pi ^2}({h^2} + 32h + 256)}}{{250\sqrt h }}} {\text{d}}h\) A1
\(t = \frac{{ - 4{\pi ^2}}}{{250}}\int {\left( {{h^{\frac{3}{2}}} + 32{h^{\frac{1}{2}}} + 256{h^{ - \frac{1}{{2}}}}} \right){\text{d}}h} \) AG
(iii) METHOD 1
\(t = \frac{{ - 4{\pi ^2}}}{{250}}\int_{48}^0 {\left( {{h^{\frac{3}{2}}} + 32{h^{\frac{1}{2}}} + 256{h^{ - \frac{1}{2}}}} \right)} {\text{d}}h\) (M1)
\(t = 2688.756 \ldots {\text{ (s)}}\) (A1)
\(45\) minutes (correct to the nearest minute) A1
METHOD 2
\(t = \frac{{ - 4{\pi ^2}}}{{250}}\left( {\frac{2}{5}{h^{\frac{5}{2}}} + \frac{{64}}{3}{h^{\frac{3}{2}}} + 512{h^{\frac{1}{2}}}} \right) + c\)
when \(t = 0,{\text{ }}h = 48 \Rightarrow c = 2688.756 \ldots \left( {c = \frac{{4{\pi ^2}}}{{250}}\left( {\frac{2}{5} \times {{48}^{\frac{5}{2}}} + \frac{{64}}{3} \times {{48}^{\frac{3}{2}}} + 512 \times {{48}^{\frac{1}{2}}}} \right)} \right)\) (M1)
when \(h = 0,{\text{ }}t = 2688.756 \ldots \left( {t = \frac{{4{\pi ^2}}}{{250}}\left( {\frac{2}{5} \times {{48}^{\frac{5}{2}}} + \frac{{64}}{3} \times {{48}^{\frac{3}{2}}} + 512 \times {{48}^{\frac{1}{2}}}} \right)} \right){\text{ (s)}}\) (A1)
45 minutes (correct to the nearest minute) A1
[10 marks]
EITHER
the depth stabilizes when \(\frac{{{\text{d}}V}}{{{\text{d}}t}} = 0\;\;\;ie\;\;\;8.5 - \frac{{250\sqrt h }}{{\pi (h + 16)}} = 0\) R1
attempting to solve \(8.5 - \frac{{250\sqrt h }}{{\pi (h + 16)}} = 0\;\;\;{\text{for }}h\) (M1)
OR
the depth stabilizes when \(\frac{{{\text{d}}h}}{{{\text{d}}t}} = 0\;\;\;ie\;\;\;\frac{1}{{4\pi (h + 16)}}\left( {8.5 - \frac{{250\sqrt h }}{{\pi (h + 16)}}} \right) = 0\) R1
attempting to solve \(\frac{1}{{4\pi (h + 16)}}\left( {8.5 - \frac{{250\sqrt h }}{{\pi (h + 16)}}} \right) = 0\;\;\;{\text{for }}h\) (M1)
THEN
\(h = 5.06{\text{ (cm)}}\) A1
[3 marks]
Total [16 marks]
Examiners report
This question was done reasonably well by a large proportion of candidates. Many candidates however were unable to show the required result in part (a). A number of candidates seemingly did not realize how the container was formed while other candidates attempted to fudge the result.
Part (b) was quite well done. In part (b) (i), most candidates were able to correctly calculate \(\frac{{{\text{d}}V}}{{{\text{d}}h}}\) and correctly apply a related rates expression to show the given result. Some candidates however made a sign error when stating \(\frac{{{\text{d}}V}}{{{\text{d}}t}}\). A large number of candidates successfully answered part (b) (ii). In part (b) (iii), successful candidates either set up and calculated an appropriate definite integral or antidifferentiated and found that \(t = C\) when \(h = 0\).
In part (c), a pleasing number of candidates realized that the water depth stabilized when either \(\frac{{{\text{d}}V}}{{{\text{d}}t}} = 0\) or \(\frac{{{\text{d}}h}}{{{\text{d}}t}} = 0\), sketched an appropriate graph and found the correct value of \(h\). Some candidates misinterpreted the situation and attempted to find the coordinates of the local minimum of their graph.

