| Date | May 2014 | Marks available | 5 | Reference code | 14M.2.hl.TZ1.5 |
| Level | HL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find and Write down | Question number | 5 | Adapted from | N/A |
Question
The shaded region S is enclosed between the curve \(y = x + 2\cos x\), for \(0 \leqslant x \leqslant 2\pi \), and the line \(y = x\), as shown in the diagram below.
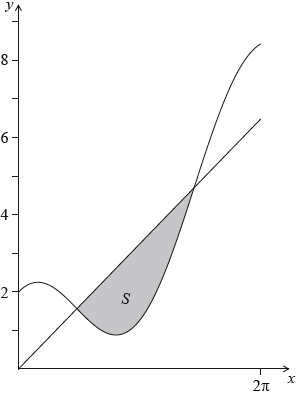
Find the coordinates of the points where the line meets the curve.
The region \(S\) is rotated by \(2\pi \) about the \(x\)-axis to generate a solid.
(i) Write down an integral that represents the volume \(V\) of the solid.
(ii) Find the volume \(V\).
Markscheme
(a) \(\frac{\pi }{2}(1.57),{\text{ }}\frac{{3\pi }}{2}(4.71)\) A1A1
hence the coordinates are \(\left( {\frac{\pi }{2},{\text{ }}\frac{\pi }{2}} \right),{\text{ }}\left( {\frac{{3\pi }}{2},{\text{ }}\frac{{3\pi }}{2}} \right)\) A1
[3 marks]
(i) \(\pi \int_{\frac{\pi }{2}}^{\frac{{3\pi }}{2}} {\left( {{x^2} - {{(x + 2\cos x)}^2}} \right){\text{d}}x} \) A1A1A1
Note: Award A1 for \({x^2} - {(x + 2\cos x)^2}\), A1 for correct limits and A1 for \(\pi \).
(ii) \(6{\pi ^2}{\text{ }}( = 59.2)\) A2
Notes: Do not award ft from (b)(i).
[5 marks]

