| Date | November 2014 | Marks available | 4 | Reference code | 14N.1.hl.TZ0.7 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 7 | Adapted from | N/A |
Question
Consider two functions \(f\) and \(g\) and their derivatives \(f'\) and \(g'\). The following table shows the values for the two functions and their derivatives at \(x = 1\), \(2\) and \(3\).
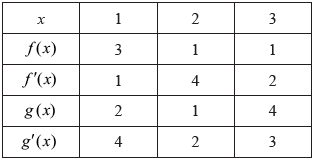
Given that \(p(x) = f(x)g(x)\) and \(h(x) = g \circ f(x)\), find
\(p'(3)\);
\(h'(2)\).
Markscheme
\(p'(3) = f'(3)g(3) + g'(3)f(3)\) (M1)
Note: Award M1 if the derivative is in terms of \(x\) or \(3\).
\( = 2 \times 4 + 3 \times 1\)
\( = 11\) A1
[2 marks]
\(h'(x) = g'\left( {f(x)} \right)f'(x)\) (M1)(A1)
\(h'(2) = g'(1)f'(2)\) A1
\( = 4 \times 4\)
\( = 16\) A1
[4 marks]
Total [6 marks]
Examiners report
This was a problem question for many candidates. Some quite strong candidates, on the evidence of their performance on other questions, did not realise that ‘composite functions’ and ‘functions of a function’ were the same thing, and therefore that the chain rule applied.
This was a problem question for many candidates. Some quite strong candidates, on the evidence of their performance on other questions, did not realise that ‘composite functions’ and ‘functions of a function’ were the same thing, and therefore that the chain rule applied.

