| Date | May 2014 | Marks available | 15 | Reference code | 14M.2.hl.TZ2.12 |
| Level | HL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find, Hence, and Show that | Question number | 12 | Adapted from | N/A |
Question
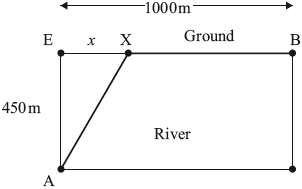
Engineers need to lay pipes to connect two cities A and B that are separated by a river of width 450 metres as shown in the following diagram. They plan to lay the pipes under the river from A to X and then under the ground from X to B. The cost of laying the pipes under the river is five times the cost of laying the pipes under the ground.
Let \({\text{EX}} = x\).
Let k be the cost, in dollars per metre, of laying the pipes under the ground.
(a) Show that the total cost C, in dollars, of laying the pipes from A to B is given by \(C = 5k\sqrt {202\,500 + {x^2}} + (1000 - x)k\).
(b) (i) Find \(\frac{{{\text{d}}C}}{{{\text{d}}x}}\).
(ii) Hence find the value of x for which the total cost is a minimum, justifying that this value is a minimum.
(c) Find the minimum total cost in terms of k.
The angle at which the pipes are joined is \({\rm{A\hat XB}} = \theta \).
(d) Find \(\theta \) for the value of x calculated in (b).
For safety reasons \(\theta \) must be at least 120°.
Given this new requirement,
(e) (i) find the new value of x which minimises the total cost;
(ii) find the percentage increase in the minimum total cost.
Markscheme
(a) \(C = {\text{AX}} \times 5k + {\text{XB}} \times k\) (M1)
Note: Award (M1) for attempting to express the cost in terms of AX, XB and k.
\( = 5k\sqrt {{{450}^2} + {x^2}} + (1000 - x)k\) A1
\( = 5k\sqrt {202\,500 + {x^2}} + (1000 - x)k\) AG
[2 marks]
(b) (i) \(\frac{{{\text{d}}C}}{{{\text{d}}x}} = k\left[ {\frac{{5 \times 2x}}{{2\sqrt {202\,500 + {x^2}} }} - 1} \right] = k\left( {\frac{{5x}}{{\sqrt {202\,500 + {x^2}} }} - 1} \right)\) M1A1
Note: Award M1 for an attempt to differentiate and A1 for the correct derivative.
(ii) attempting to solve \(\frac{{{\text{d}}C}}{{{\text{d}}x}} = 0\) M1
\(\frac{5}{{\sqrt {202\,500 + {x^2}} }} = 1\) (A1)
\(x = 91.9{\text{ (m) }}\left( { = \frac{{75\sqrt 6 }}{2}{\text{ (m)}}} \right)\) A1
METHOD 1
for example,
at \(x = 91\frac{{{\text{d}}C}}{{{\text{d}}x}} = - 0.00895k < 0\) M1
at \(x = 92\frac{{{\text{d}}C}}{{{\text{d}}x}} = 0.001506k > 0\) A1
Note: Award M1 for attempting to find the gradient either side of \(x = 91.9\) and A1 for two correct values.
thus \(x = 91.9\) gives a minimum AG
METHOD 2
\(\frac{{{{\text{d}}^2}C}}{{{\text{d}}{x^2}}} = \frac{{1\,012\,500k}}{{{{\left( {{x^2} + 202\,500} \right)}^{\frac{3}{2}}}}}\)
at \(x = 91.9\frac{{{{\text{d}}^2}C}}{{{\text{d}}{x^2}}} = 0.010451k > 0\) (M1)A1
Note: Award M1 for attempting to find the second derivative and A1 for the correct value.
Note: If \(\frac{{{{\text{d}}^2}C}}{{{\text{d}}{x^2}}}\) is obtained and its value at \(x = 91.9\) is not calculated, award (M1)A1 for correct reasoning eg, both numerator and denominator are positive at \(x = 91.9\).
thus \(x = 91.9\) gives a minimum AG
METHOD 3
Sketching the graph of either C versus x or \(\frac{{{\text{d}}C}}{{{\text{d}}x}}\) versus x. M1
Clearly indicating that \(x = 91.9\) gives the minimum on their graph. A1
[7 marks]
(c) \({C_{\min }} = 3205k\) A1
Note: Accept 3200k.
Accept 3204k.
[1 mark]
(d) \(\arctan \left( {\frac{{450}}{{91.855865{\text{K}}}}} \right) = 78.463{\text{K}}^\circ \) M1
\(180 - 78.463{\text{K = 101.537K}}\)
\( = 102^\circ \) A1
[2 marks]
(e) (i) when \(\theta = 120^\circ ,{\text{ }}x = 260{\text{ (m) }}\left( {\frac{{450}}{{\sqrt 3 }}{\text{ (m)}}} \right)\) A1
(ii) \(\frac{{133.728{\text{K}}}}{{3204.5407685{\text{K}}}} \times 100\% \) M1
\( = 4.17{\text{ (% )}}\) A1
[3 marks]
Total [15 marks]

