| Date | November 2017 | Marks available | 4 | Reference code | 17N.1.hl.TZ0.9 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Show that | Question number | 9 | Adapted from | N/A |
Question
In the following diagram, \(\overrightarrow {{\text{OA}}} \) = a, \(\overrightarrow {{\text{OB}}} \) = b. C is the midpoint of [OA] and \(\overrightarrow {{\text{OF}}} = \frac{1}{6}\overrightarrow {{\text{FB}}} \).
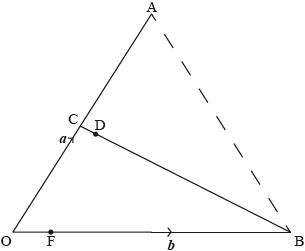
It is given also that \(\overrightarrow {{\text{AD}}} = \lambda \overrightarrow {{\text{AF}}} \) and \(\overrightarrow {{\text{CD}}} = \mu \overrightarrow {{\text{CB}}} \), where \(\lambda ,{\text{ }}\mu \in \mathbb{R}\).
Find, in terms of a and b \(\overrightarrow {{\text{OF}}} \).
Find, in terms of a and b \(\overrightarrow {{\text{AF}}} \).
Find an expression for \(\overrightarrow {{\text{OD}}} \) in terms of a, b and \(\lambda \);
Find an expression for \(\overrightarrow {{\text{OD}}} \) in terms of a, b and \(\mu \).
Show that \(\mu = \frac{1}{{13}}\), and find the value of \(\lambda \).
Deduce an expression for \(\overrightarrow {{\text{CD}}} \) in terms of a and b only.
Given that area \(\Delta {\text{OAB}} = k({\text{area }}\Delta {\text{CAD}})\), find the value of \(k\).
Markscheme
\(\overrightarrow {{\text{OF}}} = \frac{1}{7}\)b A1
[1 mark]
\(\overrightarrow {{\text{AF}}} = \overrightarrow {{\text{OF}}} - \overrightarrow {{\text{OA}}} \) (M1)
\( = \frac{1}{7}\)b – a A1
[2 marks]
\(\overrightarrow {{\text{OD}}} = \) a \( + \lambda \left( {\frac{1}{7}b -a} \right){\text{ }}\left( { = (1 - \lambda )a + \frac{\lambda }{7}b} \right)\) M1A1
[2 marks]
\(\overrightarrow {{\text{OD}}} = \frac{1}{2}\) a \( + \mu \left( { - \frac{1}{2}a + b} \right){\text{ }}\left( { = \left( {\frac{1}{2} - \frac{\mu }{2}} \right)a + \mu b} \right)\) M1A1
[2 marks]
equating coefficients: M1
\(\frac{\lambda }{7} = \mu ,{\text{ }}1 - \lambda = \frac{{1 - \mu }}{2}\) A1
solving simultaneously: M1
\(\lambda = \frac{7}{{13}},{\text{ }}\mu = \frac{1}{{13}}\) A1AG
[4 marks]
\(\overrightarrow {{\text{CD}}} = \frac{1}{{13}}\overrightarrow {{\text{CB}}} \)
\( = \frac{1}{{13}}\left( {b - \frac{1}{2}a} \right){\text{ }}\left( { = - \frac{1}{{26}}a + \frac{1}{{13}}b} \right)\) M1A1
[2 marks]
METHOD 1
\({\text{area }}\Delta {\text{ACD}} = \frac{1}{2}{\text{CD}} \times {\text{AC}} \times \sin {\rm{A\hat CB}}\) (M1)
\({\text{area }}\Delta {\text{ACB}} = \frac{1}{2}{\text{CB}} \times {\text{AC}} \times \sin {\rm{A\hat CB}}\) (M1)
\({\text{ratio }}\frac{{{\text{area }}\Delta {\text{ACD}}}}{{{\text{area }}\Delta {\text{ACB}}}} = \frac{{{\text{CD}}}}{{{\text{CB}}}} = \frac{1}{{13}}\) A1
\(k = \frac{{{\text{area }}\Delta {\text{OAB}}}}{{{\text{area }}\Delta {\text{CAD}}}} = \frac{{13}}{{{\text{area }}\Delta {\text{CAB}}}} \times {\text{area }}\Delta {\text{OAB}}\) (M1)
\( = 13 \times 2 = 26\) A1
METHOD 2
\({\text{area }}\Delta {\text{OAB}} = \frac{1}{2}\left| {a \times b} \right|\) A1
\({\text{area }}\Delta {\text{CAD}} = \frac{1}{2}\left| {\overrightarrow {{\text{CA}}} \times \overrightarrow {{\text{CD}}} } \right|\) or \(\frac{1}{2}\left| {\overrightarrow {{\text{CA}}} \times \overrightarrow {{\text{AD}}} } \right|\) M1
\( = \frac{1}{2}\left| {\frac{1}{2}a \times \left( { - \frac{1}{{26}}a + \frac{1}{{13}}b} \right)} \right|\)
\( = \frac{1}{2}\left| {\frac{1}{2}a \times \left( { - \frac{1}{{26}}a} \right) + \frac{1}{2}a \times \frac{1}{{13}}b} \right|\) (M1)
\( = \frac{1}{2} \times \frac{1}{2} \times \frac{1}{{13}}\left| {a \times b} \right|{\text{ }}\left( { = \frac{1}{{52}}\left| {a \times b} \right|} \right)\) A1
\({\text{area }}\Delta {\text{OAB}} = k({\text{area }}\Delta {\text{CAD}})\)
\(\frac{1}{2}\left| {a \times b} \right| = k\frac{1}{{52}}\left| {a \times b} \right|\)
\(k = 26\) A1
[5 marks]

