| Date | November 2017 | Marks available | 8 | Reference code | 17N.1.hl.TZ0.7 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Determine | Question number | 7 | Adapted from | N/A |
Question
The folium of Descartes is a curve defined by the equation \({x^3} + {y^3} - 3xy = 0\), shown in the following diagram.
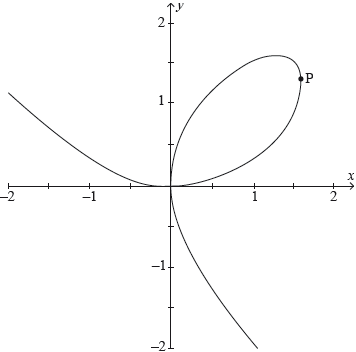
Determine the exact coordinates of the point P on the curve where the tangent line is parallel to the \(y\)-axis.
Markscheme
\({x^3} + {y^3} - 3xy = 0\)
\(3{x^2} + 3{y^2}\frac{{{\text{d}}y}}{{{\text{d}}x}} - 3x\frac{{{\text{d}}y}}{{{\text{d}}x}} - 3y = 0\) M1A1
Note: Differentiation wrt \(y\) is also acceptable.
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{3y - 3{x^2}}}{{3{y^2} - 3x}}{\text{ }}\left( { = \frac{{y - {x^2}}}{{{y^2} - x}}} \right)\) (A1)
Note: All following marks may be awarded if the denominator is correct, but the numerator incorrect.
\({y^2} - x = 0\) M1
EITHER
\(x = {y^2}\)
\({y^6} + {y^3} - 3{y^3} = 0\) M1A1
\({y^6} - 2{y^3} = 0\)
\({y^3}({y^3} - 2) = 0\)
\((y \ne 0)\therefore y = \sqrt[3]{2}\) A1
\(x = {\left( {\sqrt[3]{2}} \right)^2}{\text{ }}\left( { = \sqrt[3]{4}} \right)\) A1
OR
\({x^3} + xy - 3xy = 0\) M1
\(x({x^2} - 2y) = 0\)
\(x \ne 0 \Rightarrow y = \frac{{{x^2}}}{2}\) A1
\({y^2} = \frac{{{x^4}}}{4}\)
\(x = \frac{{{x^4}}}{4}\)
\(x({x^3} - 4) = 0\)
\((x \ne 0)\therefore x = \sqrt[3]{4}\) A1
\(y = \frac{{{{\left( {\sqrt[3]{4}} \right)}^2}}}{2} = \sqrt[3]{2}\) A1
[8 marks]

