| Date | May 2017 | Marks available | 2 | Reference code | 17M.2.hl.TZ2.4 |
| Level | HL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
Find the set of values of \(k\) that satisfy the inequality \({k^2} - k - 12 < 0\).
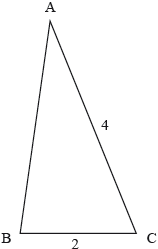
The triangle ABC is shown in the following diagram. Given that \(\cos B < \frac{1}{4}\), find the range of possible values for AB.
Markscheme
\({k^2} - k - 12 < 0\)
\((k - 4)(k + 3) < 0\) (M1)
\( - 3 < k < 4\) A1
[2 marks]
\(\cos B = \frac{{{2^2} + {c^2} - {4^2}}}{{4c}}{\text{ }}({\text{or }}16 = {2^2} + {c^2} - 4c\cos B)\) M1
\( \Rightarrow \frac{{{c^2} - 12}}{{4c}} < \frac{1}{4}\) A1
\( \Rightarrow {c^2} - c - 12 < 0\)
from result in (a)
\(0 < {\text{AB}} < 4\) or \( - 3 < {\text{AB}} < 4\) (A1)
but AB must be at least 2
\( \Rightarrow 2 < {\text{AB}} < 4\) A1
Note: Allow \( \leqslant {\text{AB}}\) for either of the final two A marks.
[4 marks]

