| Date | May 2015 | Marks available | 7 | Reference code | 15M.2.hl.TZ1.10 |
| Level | HL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 10 | Adapted from | N/A |
Question
A function \(f\) is defined by \(f(x) = (x + 1)(x-1)(x-5),{\text{ }}x \in \mathbb{R}\).
Find the values of \(x\) for which \(f(x) < \left| {f(x)} \right|\).
A function \(g\) is defined by \(g(x) = {x^2} + x - 6,{\text{ }}x \in \mathbb{R}\).
Find the values of \(x\) for which \(g(x) < \frac{1}{{g(x)}}\).
Markscheme
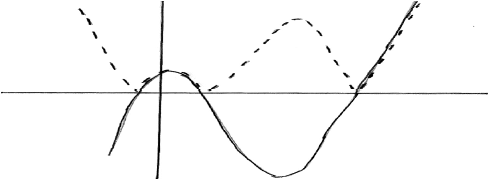
as roots of \(f(x) = 0\) are \( - 1,{\text{ }}1,{\text{ }}5\) (M1)
solution is \(\left] { - \infty ,{\text{ }} - 1} \right[ \cup \left] {1,{\text{ }}5} \right[\;\;\;(x < - 1\;\;\;{\text{or}}\;\;\;1 < x < 5)\) A1A1
Note: Award A1A0 for closed intervals.
[3 marks]
METHOD 1
\(\left( {{\text{graphs of }}g(x){\text{ and }}\frac{1}{{g(x)}}} \right)\)

roots of \(g(x) = 0\) are \( - 3\) and 2 (M1)(A1)
Notes: Award M1 if quadratic graph is drawn or two roots obtained.
Roots may be indicated anywhere eg asymptotes on graph or in inequalities below.
the intersections of the graphs \(g(x)\) and of \(1/g(x)\)
are \( - 3.19,{\text{ }} - 2.79,{\text{ }}1.79,{\text{ 2.19}}\) (M1)(A1)
Note: Award A1 for at least one of the values above seen anywhere.
solution is \(\left] { - 3.19,{\text{ }} - 3} \right[ \cup \left] { - 2.79,{\text{ }}1.79} \right[ \cup \left] {2,{\text{ }}2.19} \right[\)
\(( - 3.19 < x < - 3\;\;\;{\text{or}}\;\;\; - 2.79 < x < 1.79\;\;\;{\text{or}}\;\;\;2 < x < 2.19)\) A1A1A1
Note: Award A1A1A0 for closed intervals.
METHOD 2
\(\left( {{\text{graph of }}g(x) - \frac{1}{{g(x)}}} \right)\)
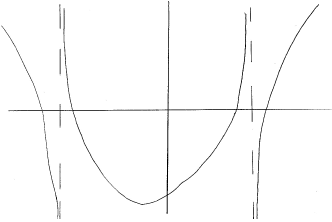
asymptotes at \(x = - 3\) and \(x = 2\) (M1)(A1)
Note: May be indicated on the graph.
roots of graph are \( - 3.19,{\text{ }} - 2.79,{\text{ }}1.79,{\text{ }}2.19\) (M1)(A1)
Note: Award A1 for at least one of the values above seen anywhere.
solution is (when graph is negative)
\(\left] { - 3.19,{\text{ }} - 3} \right[ \cup \left] { - 2.79,{\text{ }}1.79} \right[ \cup \left] {2,{\text{ }}2.19} \right[\)
\(( - 3.19 < x < - 3\;\;\;{\text{or}}\;\;\; - 2.79 < x < 1.79\;\;\;{\text{or}}\;\;\;2 < x < 2.19)\) A1A1A1
Note: Award A1A1A0 for closed intervals.
[7 marks]
Total [10 marks]
Examiners report
In general part (a) was performed correctly, with the vast majority of candidates stating the correct open intervals as required.
In part (b) many candidates scored a few marks by just finding intersection points and equations of asymptotes; many other candidates showed difficulties in manipulating inequalities and ignored the fact that the quantities could be negative. Candidates that used the graph well managed to achieve full marks. Unfortunately many sketches were very crudely drawn hence they were of limited value for assessment purposes.

