| Date | November 2016 | Marks available | 5 | Reference code | 16N.3dm.hl.TZ0.4 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
The simple, complete graph \({\kappa _n}(n > 2)\) has vertices \({{\text{A}}_1},{\text{ }}{{\text{A}}_2},{\text{ }}{{\text{A}}_3},{\text{ }} \ldots ,{\text{ }}{{\text{A}}_n}\). The weight of the edge from \({{\text{A}}_i}\) to \({{\text{A}}_j}\) is given by the number \(i + j\).
Consider the general graph \({\kappa _n}\).
(i) Draw the graph \({\kappa _4}\) including the weights of all the edges.
(ii) Use the nearest-neighbour algorithm, starting at vertex \({{\text{A}}_1}\), to find a Hamiltonian cycle.
(iii) Hence, find an upper bound to the travelling salesman problem for this weighted graph.
Consider the graph \({\kappa _5}\). Use the deleted vertex algorithm, with \({{\text{A}}_5}\) as the deleted vertex, to find a lower bound to the travelling salesman problem for this weighted graph.
(i) Use the nearest-neighbour algorithm, starting at vertex \({{\text{A}}_1}\), to find a Hamiltonian cycle.
(ii) Hence find and simplify an expression in \(n\), for an upper bound to the travelling salesman problem for this weighted graph.
By splitting the weight of the edge \({{\text{A}}_i}{{\text{A}}_j}\) into two parts or otherwise, show that all Hamiltonian cycles of \({\kappa _n}\) have the same total weight, equal to the answer found in (c)(ii).
Markscheme
(i) 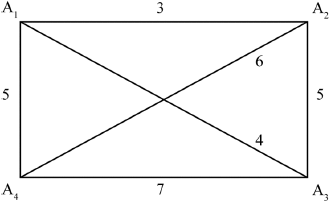 A1A1
A1A1
Note: A1 for the graph, A1 for the weights.
(ii) cycle is \({{\text{A}}_1}{{\text{A}}_2}{{\text{A}}_3}{{\text{A}}_4}{{\text{A}}_1}\) A1
(iii) upper bound is \(3 + 5 + 7 + 5 = 20\) A1
[4 marks]
with \({{\text{A}}_5}\) deleted, (applying Kruskal’s Algorithm) the minimum spanning tree will consist of the edges \({{\text{A}}_1}{{\text{A}}_2},{\text{ }}{{\text{A}}_1}{{\text{A}}_3}{\text{, }}{{\text{A}}_1}{{\text{A}}_4}\), of weights 3, 4, 5 (M1)A1
the two edges of smallest weight from \({{\text{A}}_5}\) are \({{\text{A}}_5}{{\text{A}}_1}\) and \({{\text{A}}_5}{{\text{A}}_2}\) of weights 6 and 7 (M1)A1
so lower bound is \(3 + 4 + 5 + 6 + 7 = 25\) A1
[5 marks]
(i) starting at \({{\text{A}}_1}\) we go \({{\text{A}}_2},{\text{ }}{{\text{A}}_3}{\text{ }} \ldots {\text{ }}{{\text{A}}_n}\)
we now have to take \({{\text{A}}_n}{{\text{A}}_1}\)
thus the cycle is \({{\text{A}}_1}{{\text{A}}_2}{{\text{A}}_3} \ldots {{\text{A}}_{n - 1}}{{\text{A}}_n}{{\text{A}}_1}\) A1A1
Note: Final A1 is for \({{\text{A}}_n}{{\text{A}}_1}\).
(ii) smallest edge from \({{\text{A}}_1}\) is \({{\text{A}}_1}{{\text{A}}_2}\) of weight 3, smallest edge from \({{\text{A}}_2}\) (to a new vertex) is \({{\text{A}}_2}{{\text{A}}_3}\) of weight 5, smallest edge from \({{\text{A}}_{n - 1}}\) (to a new vertex) is \({{\text{A}}_{n - 1}}{{\text{A}}_n}\) of weight \(2n - 1\) (M1)
weight of \({{\text{A}}_n}{{\text{A}}_1}\) is \(n + 1\)
weight is \(3 + 5 + 7 + \ldots + (2n - 1) + (n + 1)\) A1
\( = \frac{{(n - 1)}}{2}(2n + 2) + (n + 1)\) M1A1
\( = n(n + 1)\) (which is an upper bound) A1
Note: Follow through is not applicable.
[7 marks]
put a marker on each edge \({{\text{A}}_i}{{\text{A}}_j}\) so that \(i\) of the weight belongs to vertex \({{\text{A}}_i}\) and \(j\) of the weight belongs to vertex \({{\text{A}}_j}\) M1
the Hamiltonian cycle visits each vertex once and only once and for vertex \({{\text{A}}_i}\) there will be weight \(i\) (belonging to vertex \({{\text{A}}_i}\)) both going in and coming out R1
so the total weight will be \(\sum\limits_{i = 1}^n {2i = 2\frac{n}{2}(n + 1) = n(n + 1)} \) A1AG
Note: Accept other methods for example induction.
[3 marks]

