| Date | May 2016 | Marks available | 5 | Reference code | 16M.3dm.hl.TZ0.2 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Find | Question number | 2 | Adapted from | N/A |
Question
The weights of the edges in the complete graph \(G\) are shown in the following table.
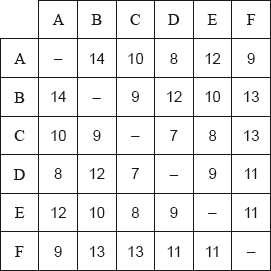
Starting at A, use the nearest neighbour algorithm to find an upper bound for the travelling salesman problem for \(G\).
By first removing A , use the deleted vertex algorithm to find a lower bound for the travelling salesman problem for \(G\).
Markscheme
attempt to use the nearest neighbour algorithm M1
\(\begin{array}{*{20}{l}} {{\text{the nearest neighbour path is}}}&{{\text{A}} \to {\text{D}} \to {\text{C }}A1} \\ {}&{ \to {\text{E}} \to {\text{B}} \to {\text{F}} \to {\text{A }}A1} \end{array}\)
the upper bound is the total weight of this path, ie (M1)
\(8 + 7 + 8 + 10 + 13 + 9 = 55\) A1
Note: The (M1) is for adding 6 weights together.
[5 marks]
attempt to use an appropriate algorithm, with A deleted, to determine the minimum spanning tree, eg Kruskal’s (M1)
CD (7) A1
CE, CB (8,9) A1
DF or EF (11) A1
the weight of this minimum spanning tree is 35 (A1)
adding in the two smallest weights joining A (AD and AF) to this tree gives a lower bound (M1)
of \(35 + 8 + 9 = 52\) A1
Note: Clear diagrams aiding solutions are acceptable in (a) and (b).
[7 marks]
Examiners report
Generally good use of the nearest neighbour algorithm. Some candidates showed no knowledge of it and there was some confusion with the twice the weight of a minimal spanning tree method. Some candidates forgot to go back to A and thus did not have a Hamiltonian cycle.
The method was generally known. Some candidates used nearest neighbour instead of Kruskal’s algorithm to find a minimal spanning tree. Some forgot to add in the two edges connected to . Some with the right method made mistakes in not noticing the correct edge to choose. A

