| Date | November 2013 | Marks available | 7 | Reference code | 13N.3dm.hl.TZ0.1 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Find and Sketch | Question number | 1 | Adapted from | N/A |
Question
The following diagram shows a weighted graph.
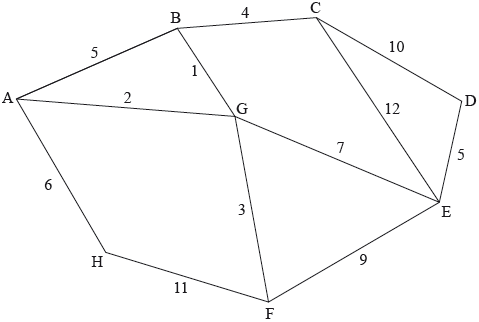
(a) Use Kruskal’s algorithm to find a minimum spanning tree, clearly showing the order in which the edges are added.
(b) Sketch the minimum spanning tree found, and write down its weight.
Markscheme
(a) use Kruskal’s algorithm: begin by choosing the shortest edge and then select a sequence of edges of non-decreasing weights, checking at each stage that no cycle is completed (M1)
| choice | edge | weight |
| 1 | BG | 1 |
| 2 | AG | 2 |
| 3 | FG | 3 |
| 4 | BC | 4 |
| 5 | DE | 5 |
| 6 | AH | 6 |
| 7 | EG | 7 |
A1
A3
Note: A1 for steps 2–4, A1for step 5 and A1for steps 6, 7.
Award marks only if it is clear that Kruskal’s algorithm is being used.
[5 marks]
(b) weight \( = 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28\) A1
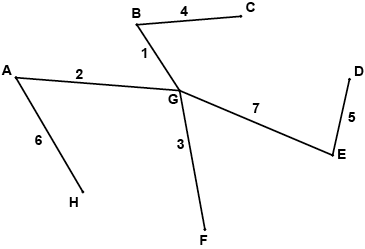 A1
A1
Note: Award FT only if it is a spanning tree.
[2 marks]
Examiners report
Well answered by the majority of candidates.

