| Date | November 2015 | Marks available | 5 | Reference code | 15N.3dm.hl.TZ0.1 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
The distances by road, in kilometres, between towns in Switzerland are shown in the following table.
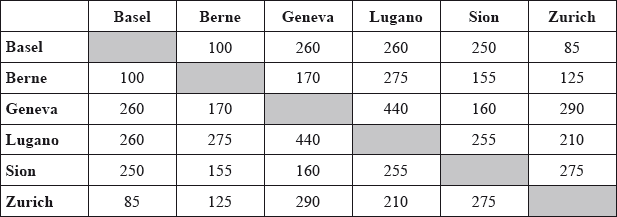
A cable television company wishes to connect the six towns placing cables along the road system.
Use Kruskal’s algorithm to find the minimum length of cable needed to connect the six towns.
Visitors to Switzerland can visit some principal locations for tourism by using a network of scenic railways as represented by the following graph:
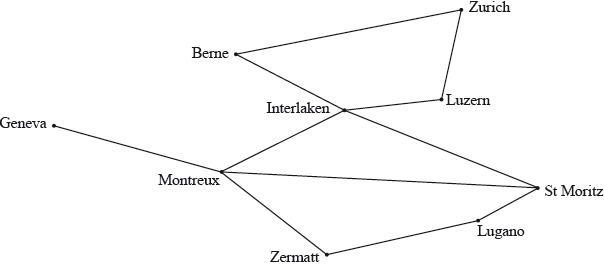
(i) State whether the graph has any Hamiltonian paths or Hamiltonian cycles, justifying your answers.
(ii) State whether the graph has any Eulerian trails or Eulerian circuits, justifying your answers.
(iii) The tourist board would like to make it possible to arrive in Geneva, travel all the available scenic railways, exactly once, and depart from Zurich. Find which locations would need to be connected by a further scenic railway in order to make this possible.
Markscheme
Zurich-Basel 85 M1A1
Berne-Basel 100 A1
Sion-Berne 155
Sion-Geneva 160
Zurich-Lugano 210 A1
total length of pipe needed is 710 km A1
Note: Award M1 for attempt to start with smallest length.
Note: Accept graphical solution showing lengths chosen.
Note: Award N1 for a correct spanning tree and N1 for 710 km with no method shown.
[6 marks]
(i) possible Hamiltonian path eg Geneva-Montreux-Zermatt-Lugano-St Moritz-Interlaken-Luzern-Zurich-Berne A1
no possible Hamiltonian cycles eg we would have to pass through Montreux twice as Geneva is only connected to Montreux or Interlaken twice R1
(ii) possible Eulerian trail as there are 2 odd vertices (Geneva and St Moritz) R1
no possible Eulerian circuits as not all even vertices R1
Note: Accept an example of a Eulerian trail for the first R1.
(iii) St Moritz to Zurich A2
Note: If St Moritz and Zurich are connected via existing edges award A1.
[6 marks]
Total [11 marks]

