| Date | November 2014 | Marks available | 7 | Reference code | 14N.3dm.hl.TZ0.3 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Find, State, and Use | Question number | 3 | Adapted from | N/A |
Question
The following graph represents the cost in dollars of travelling by bus between 10 towns in a particular province.
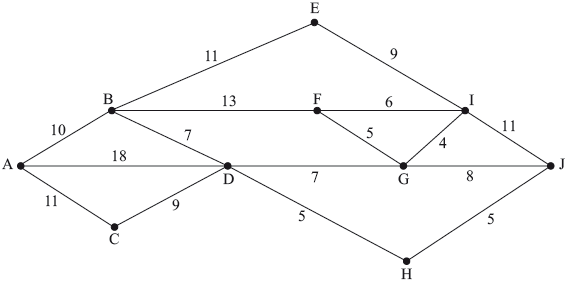
Use Dijkstra’s algorithm to find the cheapest route between \(A\) and \(J\), and state its cost.
For the remainder of the question you may find the cheapest route between any two towns by inspection.
It is given that the total cost of travelling on all the roads without repeating any is \(\$ 139\).
A tourist decides to go over all the roads at least once, starting and finishing at town \(A\).
Find the lowest possible cost of his journey, stating clearly which roads need to be travelled more than once. You must fully justify your answer.
Markscheme
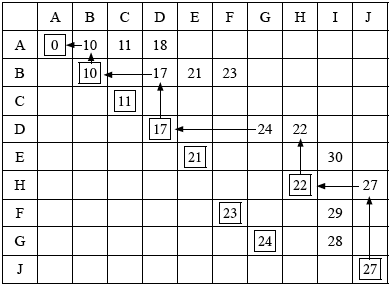M1A1A1A1
(M1 for an attempt at Dijkstra’s)
(A1 for value of \({\text{D}} = 17\))
(A1 for value of \({\text{H}} = 22\))
(A1 for value of \({\text{G}} = 22\))
route is \(ABDHJ\) (M1)A1
cost is \($27\) A1
Note: Accept other layouts.
[7 marks]
there are 4 odd vertices \(A\), \(D\), \(F\) and \(J\) A1
these can be joined up in 3 ways with the following extra costs
\(AD\) and \(FJ\)\(\;\;\;17 + 13 = 30\)
\(AF\) and \(DJ\)\(\;\;\;23 + 10 = 33\)
\(AJ\) and \(DF\)\(\;\;\;27 + 12 = 39\) M1A1A1
Note: Award M1 for an attempt to find different routes.
Award A1A1 for correct values for all three costs A1 for one correct.
need to repeat \(AB\), \(BD\), \(FG\) and \(GJ\) A1
total cost is \(139 + 30 = \$ 169\) A1
[6 marks]
Total [13 marks]
Examiners report
Many candidates had the correct route and the cost. Not all showed sufficient working with their Dijkstra’s algorithm. See the mark-scheme for the neat way of laying out the working, including the back-tracking method. This tabular working is efficient, avoids mistakes and saves time.
There was often confusion here between this problem and the travelling salesman. Good candidates started with the number of vertices of odd degree. Weaker candidates just tried to write the answer down without complete reasoning. All the 3 ways of joining the odd vertices had to be considered so that you knew you had the smallest. Sometimes a mark was lost by giving which routes (paths) had to be repeated rather than which roads (edges).
