| Date | November 2016 | Marks available | 7 | Reference code | 16N.3dm.hl.TZ0.1 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Express and Find | Question number | 1 | Adapted from | N/A |
Question
In this question the notation \({({a_n}{a_{n - 1}} \ldots {a_2}{a_1}{a_0})_b}\) is used to represent a number in base \(b\), that has unit digit of \({a_0}\). For example \({(2234)_5}\) represents \(2 \times {5^3} + 2 \times {5^2} + 3 \times 5 + 4 = 319\) and it has a unit digit of 4.
Let \(x\) be the cube root of the base 7 number \({(503231)_7}\).
(i) By converting the base 7 number to base 10, find the value of \(x\), in base 10.
(ii) Express \(x\) as a base 5 number.
Let \(y\) be the base 9 number \({({a_n}{a_{n - 1}} \ldots {a_1}{a_0})_9}\). Show that \(y\) is exactly divisible by 8 if and only if the sum of its digits, \(\sum\limits_{i = 0}^n {{a_i}} \), is also exactly divisible by 8.
Using the method from part (b), find the unit digit when the base 9 number \({(321321321)_9}\) is written as a base 8 number.
Markscheme
(i) converting to base 10
\({(503231)_7} = 5 \times {7^5} + 3 \times {7^3} + 2 \times {7^2} + 3 \times 7 + 1 = 85184\) M1A1A1
so \(x = 44\) A1
(ii) repeated division by 5 gives (M1)
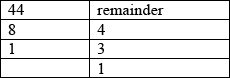
so base 5 value for \(x\) is \({(134)_5}\) A1
Notes: Alternative method is to successively subtract the largest multiple of 25 and then 5.
Follow through if they forget to take the cube root and obtain \({(10211214)_5}\) then award (M1)(A1)A1.
[7 marks]
\(9 \equiv 1(\bmod 8)\) A1
\({9^i} \equiv {1^i} \equiv 1(\bmod 8)\) \(i \in \mathbb{N}\) (M1)(A1)
\(y = {a_n}{9^n} + {a_{n - 1}}{9^{n - 1}} + \ldots + {a_1}9 + {a_0} \equiv {a_n}{1^n} + {a_{n - 1}}{1^{n - 1}} + \ldots + {a_1}1 + {a_0} \equiv \)
\({a_n} + {a_{n - 1}} + \ldots + {a_1} + {a_0} \equiv \sum\limits_{i = 0}^n {{a_i}(\bmod 8)} \) M1A1A1
so \(y = 0(\bmod 8)\) and hence divisible by 8 if and only if \(\sum\limits_{i = 0}^n {{a_i} \equiv 0(\bmod 8)} \) and hence divisible by 8 R1AG
Note: Accept alternative valid methods eg binomial expansion of \({(8 + 1)^i}\), factorization of \(({a^i} - 1)\) if they have sufficient explanation.
[7 marks]
using part (b), \({(321321321)_9} \equiv 3 + 2 + 1 + 3 + 2 + 1 + 3 + 2 + 1 = 18 \equiv 2(\bmod 8)\) M1A1
so the unit digit is 2 A1
[3 marks]

