| Date | November 2013 | Marks available | 15 | Reference code | 13N.3dm.hl.TZ0.3 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Find, Hence, and Show that | Question number | 3 | Adapted from | N/A |
Question
Consider an integer \(a\) with \((n + 1)\) digits written as \(a = {10^n}{a_n} + {10^{n - 1}}{a_{n - 1}} + \ldots + 10{a_1} + {a_0}\), where \(0 \leqslant {a_i} \leqslant 9\) for \(0 \leqslant i \leqslant n\), and \({a_n} \ne 0\).
(a) Show that \(a \equiv ({a_n} + {a_{n - 1}} + \ldots + {a_0}) ({\text{mod9}})\).
(b) Hence find all pairs of values of the single digits \(x\) and \(y\) such that the number \(a = 476x212y\) is a multiple of \(45\).
(c) (i) If \(b = 34\,390\) in base 10, show that \(b\) is \(52\,151\) written in base 9.
(ii) Hence find \({b^2}\) in base 9, by performing all the calculations without changing base.
Markscheme
(a) \(10 \equiv 1(\bmod 9) \Rightarrow {10^i} \equiv 1({\text{mod9}}),{\text{ }}i = 1,{\text{ }} ... ,{\text{ }}n\) M1A1
\( \Rightarrow {10^i}{a_i} \equiv {a_i}({\text{mod9}}),{\text{ }}i = 1,{\text{ }}n\) M1
Note: Allow \(i = 0\) but do not penalize its omission.
\( \Rightarrow ({10^n}{a_n} + {10^{n - 1}}{a_{n - 1}} + \ldots + {a_0}) \equiv ({a_n} + {a_{n - 1}} + \ldots + {a_0})({\text{mod9}})\) AG
[3 marks]
(b) \(4 + 7 + 6 + x + 2 + 1 + 2 + y = 9k,{\text{ }}k \in \mathbb{Z}\) (M1)
\( \Rightarrow (22 + x + y) \equiv 0(\bmod 9),{\text{ }} \Rightarrow (x + y) \equiv 5({\text{mod9}})\)
\( \Rightarrow x + y = 5\) or \(14\) A1
if \(5\) divides \(a\), then \(y = 0\) or \(5\) M1
so \(y = 0 \Rightarrow x = 5,{\text{ }}\left( {ie{\text{ }}(x,{\text{ }}y) = (5,{\text{ }}0)} \right)\) A1
\(y = 5 \Rightarrow x = 0\) or \(x = 9,{\text{ }}\left( {ie{\text{ }}(x,{\text{ }}y) = (0,{\text{ }}5){\text{ or }}(x,{\text{ }}y) = (9,{\text{ }}5)} \right)\) A1A1
[6 marks]
(c) (i)  (M1)A1
(M1)A1
\(b = {(52\,151)_9}\) AG
(ii) 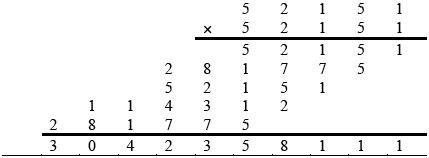 M1A3
M1A3
Note: M1 for attempt, A1 for two correct lines of multiplication, A2 for two correct lines of multiplication and a correct addition, A3 for all correct.
[6 marks]
Examiners report
Surprisingly few good answers. Part (a) had a number of correct solutions, but there were also many that seemed to be a memorised solution, not properly expressed – and consequently wrong. In part (b) many failed to understand the question, not registering that x and y were digits rather than numbers. Part (c)(i) was generally well answered, although there were a number of longer methods applied, and few managed to do (c)(ii).

