| Date | November 2016 | Marks available | 3 | Reference code | 16N.2.hl.TZ0.9 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 9 | Adapted from | N/A |
Question
The diagram shows two circles with centres at the points A and B and radii \(2r\) and \(r\), respectively. The point B lies on the circle with centre A. The circles intersect at the points C and D.
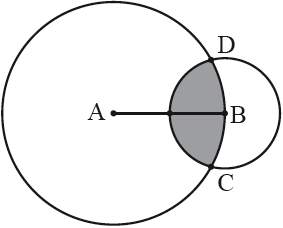
Let \(\alpha \) be the measure of the angle CAD and \(\theta \) be the measure of the angle CBD in radians.
Find an expression for the shaded area in terms of \(\alpha \), \(\theta \) and \(r\).
Show that \(\alpha = 4\arcsin \frac{1}{4}\).
Hence find the value of \(r\) given that the shaded area is equal to 4.
Markscheme
\(A = 2(\alpha - \sin \alpha ){r^2} + \frac{1}{2}(\theta - \sin \theta ){r^2}\) M1A1A1
Note: Award M1A1A1 for alternative correct expressions eg. \(A = 4\left( {\frac{\alpha }{2} - \sin \frac{\alpha }{2}} \right){r^2} + \frac{1}{2}\theta {r^2}\).
[3 marks]
METHOD 1
consider for example triangle ADM where M is the midpoint of BD M1
\(\sin \frac{\alpha }{4} = \frac{1}{4}\) A1
\(\frac{\alpha }{4} = \arcsin \frac{1}{4}\)
\(\alpha = 4\arcsin \frac{1}{4}\) AG
METHOD 2
attempting to use the cosine rule (to obtain \(1 - \cos \frac{\alpha }{2} = \frac{1}{8}\)) M1
\(\sin \frac{\alpha }{4} = \frac{1}{4}\) (obtained from \(\sin \frac{\alpha }{4} = \sqrt {\frac{{1 - \cos \frac{\alpha }{2}}}{2}} \)) A1
\(\frac{\alpha }{4} = \arcsin \frac{1}{4}\)
\(\alpha = 4\arcsin \frac{1}{4}\) AG
METHOD 3
\(\sin \left( {\frac{\pi }{2} - \frac{\alpha }{4}} \right) = 2\sin \frac{\alpha }{2}\) where \(\frac{\theta }{2} = \frac{\pi }{2} - \frac{\alpha }{4}\)
\(\cos \frac{\alpha }{4} = 4\sin \frac{\alpha }{4}\cos \frac{\alpha }{4}\) M1
Note: Award M1 either for use of the double angle formula or the conversion from sine to cosine.
\(\frac{1}{4} = \sin \frac{\alpha }{4}\) A1
\(\frac{\alpha }{4} = \arcsin \frac{1}{4}\)
\(\alpha = 4\arcsin \frac{1}{4}\) AG
[2 marks]
(from triangle ADM), \(\theta = \pi - \frac{\alpha }{2}{\text{ }}\left( { = \pi - 2\arcsin \frac{1}{4} = 2\arcsin \frac{1}{4} = 2.6362 \ldots } \right)\) A1
attempting to solve \(2(\alpha - \sin \alpha ){r^2} + \frac{1}{2}(\theta - \sin \theta ){r^2} = 4\)
with \(\alpha = 4\arcsin \frac{1}{4}\) and \(\theta = \pi - \frac{\alpha }{2}{\text{ }}\left( { = 2\arccos \frac{1}{4}} \right)\) for \(r\) (M1)
\(r = 1.69\) A1
[3 marks]

