| Date | May 2016 | Marks available | 6 | Reference code | 16M.2.hl.TZ1.4 |
| Level | HL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
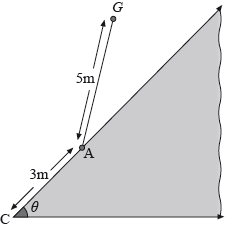
The diagram below shows a fenced triangular enclosure in the middle of a large grassy field. The points A and C are 3 m apart. A goat \(G\) is tied by a 5 m length of rope at point A on the outside edge of the enclosure.
Given that the corner of the enclosure at C forms an angle of \(\theta \) radians and the area of field that can be reached by the goat is \({\text{44 }}{{\text{m}}^{\text{2}}}\), find the value of \(\theta \).
Markscheme
attempting to use the area of sector formula (including for a semicircle) M1
semi-circle \(\frac{1}{2}\pi \times {5^2} = \frac{{25\pi }}{2} = 39.26990817 \ldots \) (A1)
angle in smaller sector is \(\pi - \theta \) (A1)
area of sector \( = \frac{1}{2} \times {2^2} \times (\pi - \theta )\) (A1)
attempt to total a sum of areas of regions to 44 (M1)
\(2(\pi - \theta ) = 44 - 39.26990817 \ldots \)
\(\theta = 0.777{\text{ }}\left( { = \frac{{29\pi }}{4} - 22} \right)\) A1
Note: Award all marks except the final A1 for correct working in degrees.
Note: Attempt to solve with goat inside triangle should lead to nonsense answer and so should only receive a maximum of the two M marks.
[6 marks]
Examiners report
Many students experienced difficulties with this question, mostly it seems through failing to understand the question. Some students left their answers in degrees, thereby losing the final mark.

