| Date | November 2014 | Marks available | 2 | Reference code | 14N.2.SL.TZ0.2 |
| Level | Standard level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Calculate | Question number | 2 | Adapted from | N/A |
Question
This question is about the internal resistance of a cell.
A circuit is used to determine the internal resistance and emf of a cell. It consists of the cell, a variable resistor, an ideal ammeter and an ideal voltmeter. The diagram shows part of the circuit with the ammeter and voltmeter missing.
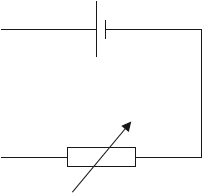
The variable resistor is set to \(1.5{\text{ }}\Omega \). When the cell converts 7.2 mJ of energy, 5.8 mC of charge moves completely around the circuit. The potential difference across the variable resistor is 0.55 V.
Define electromotive force (emf ).
Draw on the diagram the positions of the ammeter and voltmeter.
Show that the emf of the cell is 1.25 V.
Determine the internal resistance of the cell.
Calculate the energy dissipated per second in the variable resistor.
Markscheme
energy/work per unit charge supplied (by a cell) driving the current completely around a circuit;
quantity of chemical/any form of energy, per unit charge, changed to electrical energy;
potential difference across a cell when no current flows;
Allow similar responses.
ammeter in series with cell and voltmeter across cell or variable resistor; } (both needed)
\(\frac{{7.2 \times {{10}^{ - 3}}}}{{5.8 \times {{10}^{ - 3}}}}\) (= 1.24 V\(\,\,\,\)or\(\,\,\,\)1.25 V);
Answer is given so award the mark for showing the working.
\(I = \frac{{0.55}}{{1.5}}\);
\((1.25 = 0.55 + Ir){\text{ }}r = 1.9{\text{ }}\Omega \); (accept valid alternative method)
use of \({I^2}R\) or alternative;
0.20 W;
Examiners report
Very few precise answers. Most candidates almost knew what it was but were unable to define it with the necessary precision.

