| Date | November 2014 | Marks available | 3 | Reference code | 14N.2.HL.TZ0.9 |
| Level | Higher level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Determine | Question number | 9 | Adapted from | N/A |
Question
This question is in two parts. Part 1 is about the oscillation of a mass. Part 2 is about the photoelectric effect.
Part 2 Photoelectric effect
A student carries out a photoelectric experiment in which radiation is incident on a metal surface in a vacuum.
A graph of the results of the experiment show how the maximum kinetic energy \({E_{{\text{max}}}}\) of the emitted photoelectrons varies with the frequency \(f\) of the incident radiation.
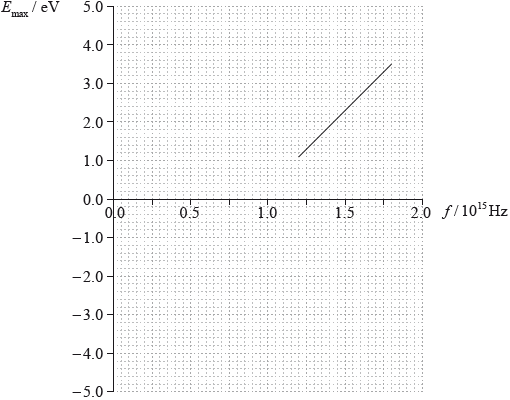
Use the graph to
Explain why photoelectrons are not emitted from the metal surface unless the frequency of incident light exceeds a minimum value.
identify the minimum value of the frequency \({f_0}\) for photoelectrons to be emitted.
determine the Planck constant.
calculate the work function, in eV, for the metal surface.
The student repeats the experiment with a different metal surface that has a smaller value
for the work function. On the graph in (e), draw a line to show how \({E_{\max }}\) varies with \(f\).
Markscheme
light consists of photons with energy \(E = hf\);
there is a minimum energy/work function required for electron to leave a particular metal;
\(hf\) must be larger than this value;
(value of intercept on \(f\)-axis =) \(9.3 \times 10^{14}\) Hz;
Allow answers in the range of 9.0 to 9.5, but with correct power of ten.
attempted use of gradient \(\left( {\frac{h}{e}} \right)\) to evaluate \(h\);
eg \(\frac{{2.4}}{{6 \times {{10}^{14}}}} = 4 \times {10^{ - 15}}{\text{ eVs}}\); (allow answers in the range of 3.9 to \(4.2 \times {10^{ - 15}}\))
\(6.4 \times {10^{ - 34}}{\text{ Js}}\); (allow ECF, eg answers in the range of 6.2 to \(6.7 \times {10^{ - 34}}\))
Do not allow a bald answer of \(6.6 \times {10^{ - 34}}\) as value is known.
or
use of y-intercept \( = \frac{{ - h{f_0}}}{e}\);
\(h = \frac{{3.77 \times 1.6 \times {{10}^{ - 19}}}}{{0.93 \times {{10}^{15}}}}\); (allow intercept between –3.6 and –3.8 eV)
\(6.4 \times {10^{ - 34}}{\text{ Js}}\); (allow ECF, eg answers in the range of 6.0 to \(6.8 \times {10^{ - 34}}\))
Do not allow a bald answer of \(6.6 \times {10^{ - 34}}\) as value is known.
\(E = 6.62 \times {10^{ - 34}} \times 9.3 \times {10^{14}}{\text{ }}( = 6.2 \times {10^{ - 19}}{\text{ J}})\);
an answer in the range of 3.4 to 4.0 eV; (allow ECF from (e)(i) and (e)(ii))
or
identifies y intercept as work function;
an answer in the range of 3.6 to 3.8 eV;
straight line of any length parallel to original data;
to left of original data, intercept on \(f\)-axis would be positive;
Examiners report
A number of candidates effectively repeated the question by stating that light had to exceed a threshold frequency to cause photoemission. To gain both marks they were expected to refer to the need for photon energy \((hf)\) to be greater than the work function energy for the metal surface.
To determine the threshold frequency most candidates correctly extended the graph to find the intercept on the f axis. Quite large numbers of candidates misread the scale.
Various methods were used to determine h. Commonly the gradient was measured, but as always candidates seemed to be unaware that they should choose points on their line as far apart as possible. The gradient in eVs was usually correctly converted to Js.
The work function was also determined in a number of different ways. The easiest method was to use the y intercept. Most candidates did well on this question.
Almost all candidates correctly drew a line parallel and to the left of the original line.

