| Date | November 2015 | Marks available | 2 | Reference code | 15N.3.HL.TZ0.13 |
| Level | Higher level | Paper | Paper 3 | Time zone | Time zone 0 |
| Command term | Calculate | Question number | 13 | Adapted from | N/A |
Question
This question is about mass and energy.
The positive kaon \({K^ + }\) has a rest mass of \(494{\text{ MeV}}\,{{\text{c}}^{ - 2}}\).
Using the grid, sketch a graph showing how the energy of the kaon increases with speed.
The kaon is accelerated from rest through a potential difference so that its energy becomes three times its rest energy. Calculate the potential difference through which the kaon was accelerated.
The neutral kaon is unstable and one of its possible modes of decay is
\[{K^0} \to {\pi ^0} + {\pi ^0}.\]
The \({\pi ^0}\) has a rest mass of \(135{\text{ MeV}}\,{{\text{c}}^{ - 2}}\). The \({K^0}\) has a rest mass of \(498{\text{ MeV}}\,{{\text{c}}^{ - 2}}\). The \({K^0}\) is at rest before it decays. The two \({\pi ^0}\) particles move apart in opposite directions along a straight line. Determine the momentum of one of the \({\pi ^0}\) particles.
Markscheme
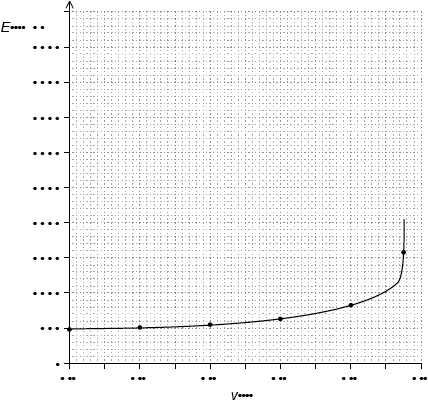
graph starting at \(E = 494\) when \(\frac{v}{c} = 0\) or a roughly horizontal line drawn until at least 0.4 c;
rises sharply/becomes asymptotic as \(\frac{v}{c}\) approaches 1;
\({E_K} = 2 \times 494{\text{ MeV}} = 988{\text{ (MeV)}}\);
potential difference \( = 988 \times {10^6}{\text{ (V)}}\) or \(1 \times {10^9}{\text{ (V)}}\);
\(pc = \left( {\sqrt {{{\left[ {\frac{E}{2}} \right]}^2} - m_0^2{c^4}} = } \right)\sqrt {{{\left[ {\frac{{498}}{2}} \right]}^2} - {{135}^2}} \);
\(p = 209{\text{ (MeV}}\,{{\text{c}}^{ - 1}})\);
Examiners report
Discriminated well between the best and average candidates, in part (a)(ii). Many weaker candidates did not distinguish between energy and kinetic energy of the particle, and often also forgot to calculate the potential difference; part (b) proved difficulty for majority of candidates, even if some very clear and good answers are among the answers of better candidates.
Discriminated well between the best and average candidates, in part (a)(ii). Many weaker candidates did not distinguish between energy and kinetic energy of the particle, and often also forgot to calculate the potential difference; part (b) proved difficulty for majority of candidates, even if some very clear and good answers are among the answers of better candidates.
Discriminated well between the best and average candidates, in part (a)(ii). Many weaker candidates did not distinguish between energy and kinetic energy of the particle, and often also forgot to calculate the potential difference; part (b) proved difficulty for majority of candidates, even if some very clear and good answers are among the answers of better candidates.

