| Date | November 2010 | Marks available | 4 | Reference code | 10N.3.HL.TZ0.H2 |
| Level | Higher level | Paper | Paper 3 | Time zone | Time zone 0 |
| Command term | Calculate | Question number | H2 | Adapted from | N/A |
Question
This question is about pair production and relativistic mechanics.
A \(\gamma \)-photon of energy 2.46 MeV is travelling close to the nucleus of a gold atom. It converts into an electron (\({{\text{e}}^ - }\)) – positron (\({{\text{e}}^ + }\)) pair. Each particle travels at 45° to the original direction of the photon.
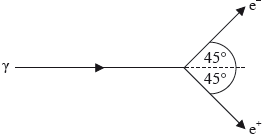
Immediately after the conversion, the kinetic energies of the electron and positron are equal. The magnitude of the recoil momentum of the gold nucleus is \(0.880{\text{ MeV}}\,{{\text{c}}^{ - 1}}\) and is in the direction of the photon.
Calculate, immediately after the decay, the magnitude of the momentum of the electron.
Calculate the value \(V\) of the potential difference through which an electron at rest must be accelerated in order to have the same magnitude of momentum as that in (a).
Markscheme
momentum of photon \( = 2.46{\text{ MeV}}\,{{\text{c}}^{ - 1}}\);
momentum of electron–positron pair \( = (2.46 - 0.880 = ){\text{ }}1.58{\text{ MeV}}\,{{\text{c}}^{ - 1}}\);
\(2{p_{{\text{electron}}}}\cos 45 = 1.58\);
\({p_{{\text{electron}}}} = \left( {\frac{{1.58}}{{2\cos 45}} = } \right){\text{ }}1.12{\text{ MeV}}\,{{\text{c}}^{ - 1}}\);
total energy of electron \( = \left( {\sqrt {{{1.12}^2} + {{0.511}^2}} = } \right){\text{ }}1.23{\text{ MeV}}\);
\({\text{KE}} = {\text{eV (}} = 1.23 - 0.511 = 0.72{\text{ MeV)}} \to V = 0.72{\text{ MV}}\);
Award [2] for bald correct answer.
Examiners report
It was rare to see correct solutions to the calculations in this question. Candidates, as in previous years did not seem familiar with handling the units \({\text{MeV}}\,{{\text{c}}^{ - 1}}\) and MeV and became confused.
It was rare to see correct solutions to the calculations in this question. Candidates, as in previous years did not seem familiar with handling the units \({\text{MeV}}\,{{\text{c}}^{ - 1}}\) and MeV and became confused.

