| Date | May 2018 | Marks available | 2 | Reference code | 18M.2.HL.TZ1.4 |
| Level | Higher level | Paper | Paper 2 | Time zone | Time zone 1 |
| Command term | Determine | Question number | 4 | Adapted from | N/A |
Question
An ohmic conductor is connected to an ideal ammeter and to a power supply of output voltage V.
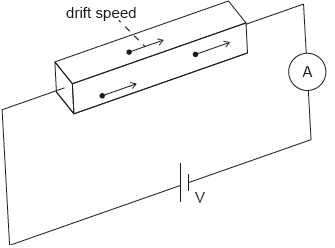
The following data are available for the conductor:
density of free electrons = 8.5 × 1022 cm−3
resistivity ρ = 1.7 × 10−8 Ωm
dimensions w × h × l = 0.020 cm × 0.020 cm × 10 cm.
The ammeter reading is 2.0 A.
The electric field E inside the sample can be approximated as the uniform electric field between two parallel plates.
Calculate the drift speed v of the electrons in the conductor in cm s–1.
Determine the electric field strength E.
Show that \(\frac{v}{E} = \frac{1}{{ne\rho }}\).
Markscheme
v «= \(\frac{I}{{neA}}\)» = \(\frac{2}{{8.5 \times {{10}^{22}} \times 1.60 \times {{10}^{ - 19}} \times {{0.02}^2}}}\)
0.37 «cms–1»
[2 marks]
V = RI = 0.086 «V»
«\(\frac{V}{d} = \frac{{0.086}}{{0.10}} = \)» 0.86 «V m–1»
Allow ECF from 4(a).
Allow ECF from MP1.
[2 marks]
ALTERNATIVE 1
clear use of Ohm’s Law (V = IR)
clear use of R = \(\frac{{\rho L}}{A}\)
combining with I = nAve and V = EL to reach result.
ALTERNATIVE 2
attempts to substitute values into equation.
correctly calculates LHS as 4.3 × 109.
correctly calculates RHS as 4.3 × 109.
For ALTERNATIVE 1 look for:
V = IR
R = \(\frac{{\rho L}}{A}\)
V = EL
I = nAve
V = I\(\frac{{\rho L}}{A}\)
EL = I\(\frac{{\rho L}}{A}\)
E = I\(\frac{\rho }{A}\)
E = nAve\(\frac{\rho }{A}\) = nveρ
\(\frac{v}{E} = \frac{1}{{ne\rho }}\)
[3 marks]

