| Date | May 2018 | Marks available | 1 | Reference code | 18M.2.HL.TZ2.9 |
| Level | Higher level | Paper | Paper 2 | Time zone | Time zone 2 |
| Command term | Show that | Question number | 9 | Adapted from | N/A |
Question
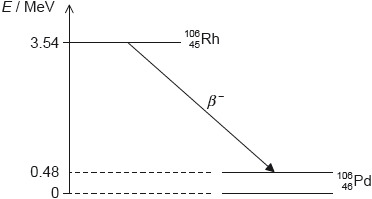
Rhodium-106 (\(_{\,\,\,45}^{106}{\text{Rh}}\)) decays into palladium-106 (\(_{\,\,\,46}^{106}{\text{Pd}}\)) by beta minus (β–) decay. The diagram shows some of the nuclear energy levels of rhodium-106 and palladium-106. The arrow represents the β– decay.
Bohr modified the Rutherford model by introducing the condition mvr = n\(\frac{h}{{2\pi }}\). Outline the reason for this modification.
Show that the speed v of an electron in the hydrogen atom is related to the radius r of the orbit by the expression
\[v = \sqrt {\frac{{k{e^2}}}{{{m_{\text{e}}}r}}} \]
where k is the Coulomb constant.
Using the answer in (b) and (c)(i), deduce that the radius r of the electron’s orbit in the ground state of hydrogen is given by the following expression.
\[r = \frac{{{h^2}}}{{4{\pi ^2}k{m_{\text{e}}}{e^2}}}\]
Calculate the electron’s orbital radius in (c)(ii).
Explain what may be deduced about the energy of the electron in the β– decay.
Suggest why the β– decay is followed by the emission of a gamma ray photon.
Calculate the wavelength of the gamma ray photon in (d)(ii).
Markscheme
the electrons accelerate and so radiate energy
they would therefore spiral into the nucleus/atoms would be unstable
electrons have discrete/only certain energy levels
the only orbits where electrons do not radiate are those that satisfy the Bohr condition «mvr = n\(\frac{h}{{2\pi }}\)»
[3 marks]
\(\frac{{{m_{\text{e}}}{v^2}}}{r} = \frac{{k{e^2}}}{{{r^2}}}\)
OR
KE = \(\frac{1}{2}\)PE hence \(\frac{1}{2}\)mev2 = \(\frac{1}{2}\frac{{k{e^2}}}{r}\)
«solving for v to get answer»
Answer given – look for correct working
[1 mark]
combining v = \(\sqrt {\frac{{k{e^2}}}{{{m_{\text{e}}}r}}} \) with mevr = \(\frac{h}{{2\pi }}\) using correct substitution
«eg \({m_e}^2\frac{{k{e^2}}}{{{m_{\text{e}}}r}}{r^2} = \frac{{{h^2}}}{{4{\pi ^2}}}\)»
correct algebraic manipulation to gain the answer
Answer given – look for correct working
Do not allow a bald statement of the answer for MP2. Some further working eg cancellation of m or r must be shown
[2 marks]
« r = \(\frac{{{{(6.63 \times {{10}^{ - 34}})}^2}}}{{4{\pi ^2} \times 8.99 \times {{10}^9} \times 9.11 \times {{10}^{ - 31}} \times {{(1.6 \times {{10}^{ - 19}})}^2}}}\)»
r = 5.3 × 10–11 «m»
[1 mark]
the energy released is 3.54 – 0.48 = 3.06 «MeV»
this is shared by the electron and the antineutrino
so the electron’s energy varies from 0 to 3.06 «MeV»
[3 marks]
the palladium nucleus emits the photon when it decays into the ground state «from the excited state»
[1 mark]
Photon energy
E = 0.48 × 106 × 1.6 × 10–19 = «7.68 × 10–14 J»
λ = «\(\frac{{hc}}{E} = \frac{{6.63 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}{{7.68 \times {{10}^{ - 14}}}}\) =» 2.6 × 10–12 «m»
Award [2] for a bald correct answer
Allow ECF from incorrect energy
[2 marks]

