| Date | May 2018 | Marks available | 1 | Reference code | 18M.2.SL.TZ1.3 |
| Level | Standard level | Paper | Paper 2 | Time zone | Time zone 1 |
| Command term | Calculate | Question number | 3 | Adapted from | N/A |
Question
A beam of coherent monochromatic light from a distant galaxy is used in an optics experiment on Earth.
The beam is incident normally on a double slit. The distance between the slits is 0.300 mm. A screen is at a distance D from the slits. The diffraction angle θ is labelled.
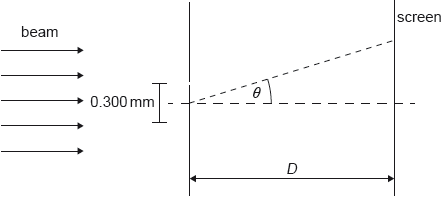
The air between the slits and the screen is replaced with water. The refractive index of water is 1.33.
A series of dark and bright fringes appears on the screen. Explain how a dark fringe is formed.
The wavelength of the beam as observed on Earth is 633.0 nm. The separation between a dark and a bright fringe on the screen is 4.50 mm. Calculate D.
Calculate the wavelength of the light in water.
State two ways in which the intensity pattern on the screen changes.
Markscheme
superposition of light from each slit / interference of light from both slits
with path/phase difference of any half-odd multiple of wavelength/any odd multiple of \(\pi \) (in words or symbols)
producing destructive interference
Ignore any reference to crests and troughs.
[3 marks]
evidence of solving for D «D = \(\frac{{sd}}{\lambda }\)»
«\(\frac{{4.50 \times {{10}^{ - 3}} \times 0.300 \times {{10}^{ - 3}}}}{{633.0 \times {{10}^{ - 9}}}}\) × 2» = 4.27 «m»
Award [1] max for 2.13 m.
[2 marks]
\(\frac{{633.0}}{{1.33}}\) = 476 «nm»
[1 mark]
distance between peaks decreases
intensity decreases
[2 marks]

