| Date | November 2009 | Marks available | 1 | Reference code | 09N.2.hl.TZ0.8 |
| Level | HL | Paper | 2 | Time zone | TZ0 |
| Command term | Suggest | Question number | 8 | Adapted from | N/A |
Question
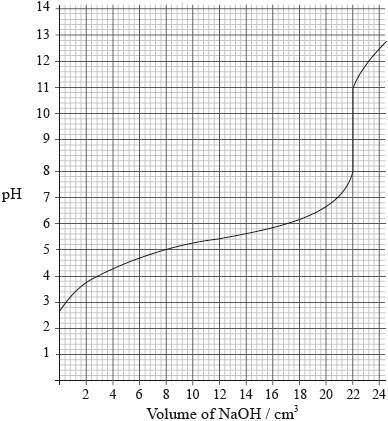
A \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) solution of a weak monoprotic acid, HA(aq), is titrated with \({\text{0.155 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide, NaOH(aq), and the following graph is obtained.
0.100 mol of ammonia, \({\text{N}}{{\text{H}}_{\text{3}}}\), was dissolved in water to make \({\text{1.00 d}}{{\text{m}}^{\text{3}}}\) of solution. This solution has a hydroxide ion concentration of \({\text{1.28}} \times {\text{1}}{{\text{0}}^{ - 3}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\).
Determine the pH at the equivalence point.
Explain, using an equation, why the equivalence point is not at \({\text{pH}} = 7\).
Calculate the concentration of the weak acid before the addition of any NaOH(aq).
Estimate, using data from the graph, the dissociation constant, \({K_{\text{a}}}\), of the weak acid, HA, showing your working.
Suggest an appropriate indicator for this titration.
Describe qualitatively the action of an acid-base indicator.
Explain what is meant by the term buffer solution.
Calculate the pH of a solution prepared by mixing \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.200 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ C}}{{\text{H}}_{\text{3}}}{\text{COOH(aq)}}\) and \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of ,\({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ NaOH(aq)}}\) showing your working.
Determine the pH of the solution.
Calculate the base dissociation constant, \({K_{\text{b}}}\), for ammonia.
Markscheme
9.5;
Accept any value in the range 9.4–9.6.
titration involves a weak acid and a strong base;
salt formed at equivalence point is basic due to hydrolysis;
\({{\text{A}}^ - }{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{HA(aq)}} + {\text{O}}{{\text{H}}^ - }{\text{(aq)}}\);
Ignore state symbols.
\(\frac{{{\text{0.155}} \times {\text{22.0}} \times {\text{1}}}}{{{\text{25.0}} \times {\text{1}}}}\);
\( = {\text{0.136 (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
at half neutralization point, \({\text{pH}} = {\text{p}}{K_{\text{a}}}\);
\({\text{p}}{K_{\text{a}}} = {\text{5.3}}\);
Accept any value in the range 5.2–5.4.
\({K_{\text{a}}} = {\text{5.0}} \times {\text{1}}{{\text{0}}^{ - 6}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
Accept calculations based on initial pH or on pH of salt.
phenolphthalein;
Accept thymolphthalein.
Allow ECF from (a)(i).
\({\text{HIn(aq)}} \rightleftharpoons {{\text{H}}^ + }{\text{(aq)}} + {\text{I}}{{\text{n}}^ - }{\text{(aq)}}\);
colour A colour B
in presence of acid/\({{\text{H}}^ + }\), equilibrium shifts to left, colour A;
in presence of base/\({\text{O}}{{\text{H}}^ - }{\text{ }}\), equilibrium shifts to right, colour B;
buffer solution resists change in pH;
on addition of small amount of acid or base;
after mixing \({\text{[C}}{{\text{H}}_3}{\text{CO}}{{\text{O}}^ - }{\text{]}} = {\text{[C}}{{\text{H}}_3}{\text{COOH]}} = {\text{0.050 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\);
\({K_{\text{a}}} = {\text{[}}{{\text{H}}^ + }{\text{]/p}}{K_{\text{a}}} = {\text{pH}}\);
\({\text{pH}} = {\text{4.76}}\);
Working must be shown to score [3].
Award [1] if 4.76 stated with no working.
\({\text{[}}{{\text{H}}^ + }{\text{]}} = \frac{{{\text{1.00}} \times {\text{1}}{{\text{0}}^{ - 14}}}}{{{\text{1.28}} \times {\text{1}}{{\text{0}}^{ - 3}}}} = {\text{7.81}} \times {\text{1}}{{\text{0}}^{ - 12}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}/{\text{pOH}} = - \log 1.28 \times {10^{ - 3}} = 2.90\);
\({\text{pH}} = (14.0 - 2.90) = 11.1\);
Award [2] for the correct final answer
\({K_{\text{b}}} = \frac{{{\text{[NH}}_4^ + {\text{][O}}{{\text{H}}^ - }{\text{]}}}}{{{\text{[N}}{{\text{H}}_3}{\text{]}}}}\);
\( = \frac{{{{(1.28 \times {{10}^{ - 3}})}^2}}}{{0.100{\text{ - }}0.00128}}/\frac{{{{(1.28 \times {{10}^{ - 3}})}^2}}}{{0.100}}\);
\( = 1.66 \times {10^{ - 5}}/1.64 \times {10^{ - 5}}\);
Examiners report
Most candidates were able to determine the pH at the equivalence point.
Salt hydrolysis was very poorly understood by many candidates and therefore they were not able to write an equation.
In part (b) most candidates described the use of indicators during titrations, but lost credit for not using the reversible equilibrium equation to explain how they function qualitatively.
Part c (ii) baffled the majority of candidates. It is surprising to see that calculations based on buffers are almost an exclusive domain of the better candidates.
In part (e), only the able candidates scored the maximum five marks for calculating the pH and the base dissociation constant for ammonia.
Overall knowledge of acid-base chemistry was considerably weak, especially calculations.

