| Date | May 2011 | Marks available | 2 | Reference code | 11M.2.sl.TZ1.7 |
| Level | SL | Paper | 2 | Time zone | TZ1 |
| Command term | Calculate | Question number | 7 | Adapted from | N/A |
Question
Carbon and silicon belong to the same group of the periodic table.
Both silicon and carbon form oxides.
State the period numbers of both carbon and silicon.
Describe and compare three features of the structure and bonding in the three allotropes of carbon: diamond, graphite and \({{\text{C}}_{{\text{60}}}}\) fullerene.
Draw the Lewis structure of \({\text{C}}{{\text{O}}_{\text{2}}}\) and predict its shape and bond angle.
Describe the structure and bonding in \({\text{Si}}{{\text{O}}_{\text{2}}}\).
Explain why silicon dioxide is a solid and carbon dioxide is a gas at room temperature.
Describe the bonding within the carbon monoxide molecule.
Silicon has three stable isotopes, \(^{{\text{28}}}{\text{Si}}\), \(^{{\text{29}}}{\text{Si}}\) and \(^{{\text{30}}}{\text{Si}}\). The heaviest isotope, \(^{{\text{30}}}{\text{Si}}\), has a percentage abundance of 3.1%. Calculate the percentage abundance of the lightest isotope to one decimal place.
Markscheme
C: 2 and Si: 3;
Award [2 max] for three of the following features:
Bonding
Graphite and C60 fullerene: covalent bonds and van der Waals’/London/dispersion forces;
Diamond: covalent bonds (and van der Waals’/London/dispersion forces);
Delocalized electrons
Graphite and C60 fullerene: delocalized electrons;
Diamond: no delocalized electrons;
Structure
Diamond: network/giant structure / macromolecular / three-dimensional structure and Graphite: layered structure / two-dimensional structure / planar;
C60 fullerene: consists of molecules / spheres made of atoms arranged in hexagons/pentagons;
Bond angles
Graphite: 120° and Diamond: 109°;
C60 fullerene: bond angles between 109–120°;
Allow Graphite: sp2 and Diamond: sp3.
Allow C60 fullerene: sp2 and sp3.
Number of atoms each carbon is bonded to
Graphite and C60 fullerene: each C atom attached to 3 others;
Diamond: each C atom attached to 4 atoms / tetrahedral arrangement of C (atoms);
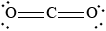
linear and 180°;
Accept crosses, lines or dots as electron pairs.
network/giant structure / macromolecular;
each Si atom bonded covalently to 4 oxygen atoms and each O atom bonded covalently to 2 Si atoms / single covalent bonds;
Award [1 max] for answers such as network-covalent, giant-covalent or macromolecular-covalent.
Both M1 and M2 can be scored by a suitable diagram.
Silicon dioxide: strong/covalent bonds in network/giant structure/macromolecule;
Carbon dioxide: weak/van der Waals’/dispersion/London forces between molecules;
triple (covalent) bond;
one electron pair donated by oxygen to carbon atom / dative (covalent)/coordinate (covalent) bond;
Award [1 max] for representation of C\(\equiv\)O.
Award [2] if CO shown with dative covalent bond.
\(2809 = 3.10 \times 30 + 28x + 29(96.9 - x)\);
\(\% {{\text{ }}^{28}}{\text{Si}} = (93 + 2810.1 - 2809) = 94.1\% \);
Award [2] for correct final answer.
Examiners report
Part (b) was exceptionally well done.
Many candidates struggled with Part (c) not being able to clearly identify the bonding and structure in the allotropes of carbon. Candidates often incorrectly discussed the properties of the allotropes.
In Part (d), candidates were competent at drawing carbon dioxide but struggled to identify the bonding and structure in silicon dioxide.
Most candidates incorrectly identifying silicon dioxide as molecular compound.
Candidates also struggled to explain why \({\text{C}}{{\text{O}}_{\text{2}}}\) was a gas and \({\text{Si}}{{\text{O}}_{\text{2}}}\) was a solid a room temperature and again commented on the properties of the compounds rather than the structure and bonding.
In part (e) many candidates failed to state that a dative bond was present in CO.
Although the calculation in (f) was more challenging than similar questions in the past, it was managed by many candidates.

