| Date | May 2015 | Marks available | 2 | Reference code | 15M.2.sl.TZ2.1 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
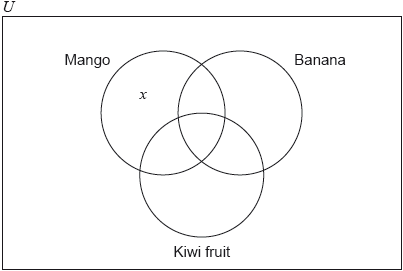
A group of 100 customers in a restaurant are asked which fruits they like from a choice of mangoes, bananas and kiwi fruits. The results are as follows.
15 like all three fruits
22 like mangoes and bananas
33 like mangoes and kiwi fruits
27 like bananas and kiwi fruits
8 like none of these three fruits
\(x\) like only mangoes
Copy the following Venn diagram and correctly insert all values from the above information.
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
Complete your Venn diagram from part (a) with this additional information in terms of \(x\).
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
Find the value of \(x\).
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
Write down the number of customers who like
(i) mangoes;
(ii) mangoes or bananas.
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
A customer is chosen at random from the 100 customers. Find the probability that this customer
(i) likes none of the three fruits;
(ii) likes only two of the fruits;
(iii) likes all three fruits given that the customer likes mangoes and bananas.
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
Two customers are chosen at random from the 100 customers. Find the probability that the two customers like none of the three fruits.
Markscheme
(A1)(A1)(A1)
Notes: Award (A1) for 15 in the correct place.
Award (A1) for 7, 18 and 12 seen in the correct places.
Award (A1) for 8 in the correct place.
Award at most (A0)(A1)(A1) if diagram is missing the rectangle.
(A1)(A1)
Notes: Award (A1) for \(x\) seen in the correct places.
Award (A1) for \(2x\) seen in the correct place.
Award (A0)(A1)(ft) if \(x\) and \(2x\) are replaced by 10 and 20 respectively.
\(2x + x + x + 15 + 8 + 7 + 18 + 12 = 100\;\;\;(4x + 60 = 100{\text{ or equivalent)}}\) (M1)
Note: Award (M1) for equating the sum of the elements of their Venn diagram to \(100\). Equating to \(100\) may be implied.
\((x = ){\text{ }}10\) (A1)(ft)(G2)
Note: Follow through from their Venn diagram. The answer must be a positive integer.
(i) \(50\) (A1)(ft)
(ii) \(82\) (A1)(ft)
Note: Follow through from their answer to part (c) and their Venn diagram.
Award (A0)(ft)(A1)(ft) if answer is \(\frac{{50}}{{100}}\) and \(\frac{{82}}{{100}}\).
(i) \(\frac{8}{{100}}\;\;\;\left( {\frac{2}{{25}};{\text{ }}0.08;{\text{ }}8\% } \right)\) (A1)
Note: Correct answer only. There is no follow through.
(ii) \(\frac{{37}}{{100}}\;\;\;(0.37,{\text{ }}37\% )\) (A1)(ft)
Note: Follow through from their Venn diagram.
(iii) \(\frac{{15}}{{22}}\;\;\;(0.681;{\text{ }}0.682;{\text{ }}68.2\% )\;\;\;(0.681818 \ldots )\) (A1)(A1)(ft)(G2)
Notes: Award (A1) for numerator, (A1)(ft) for denominator, follow through from their Venn diagram. Award (A0)(A0) if answer is given as incorrect reduced fraction without working.
\(\frac{8}{{100}} \times \frac{7}{{99}}\) (A1)(ft)(M1)
Note: Award (A1)(ft) for correct fractions, follow through from their answer to part (e)(i), (M1) for multiplying their fractions.
\( = \frac{{56}}{{9900}}\;\;\;\left( {\frac{{14}}{{2477}},{\text{ }}0.00565656 \ldots ,{\text{ }}0.00566,{\text{ }}0.0056,{\text{ }}0.566\% } \right)\) (A1)(ft)(G2)

