| Date | November 2013 | Marks available | 4 | Reference code | 13N.1.sl.TZ0.2 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Complete | Question number | 2 | Adapted from | N/A |
Question
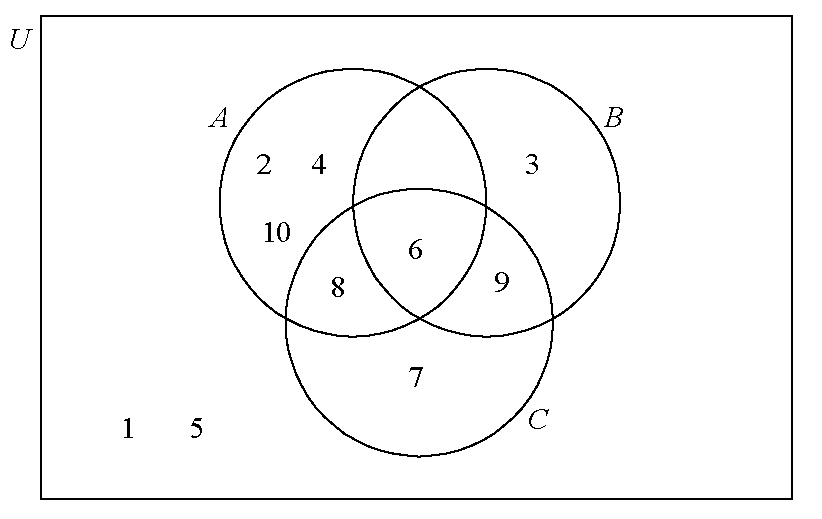
\(U\) is the set of positive integers less than or equal to \(10\).
\(A\), \(B\) and \(C\) are subsets of \(U\).
\(A = \left\{ {{\text{even integers}}} \right\}\)
\(B = \left\{ {{\text{multiples of }}3} \right\}\)
\(C = \left\{ {6,{\text{ }}7,{\text{ }}8,{\text{ }}9} \right\}\)
List the elements of \(A\).
List the elements of \(B\).
Complete the Venn diagram with all the elements of \(U\).

Markscheme
\(2, 4, 6, 8, 10\) (A1) (C1)
Note: Do not penalize the use of \(\left\{ {{\text{ }}} \right\}\).
[1 mark]
\(3, 6, 9\) (A1) (C1)
Note: Do not penalize the use of \(\left\{ {{\text{ }}} \right\}\).
Follow through from part (a) only if their \({\text{U}}\) is listed.
[1 mark]
 (A1)(ft)(A1)(ft)(A1)(ft)(A1)(ft) (C4)
(A1)(ft)(A1)(ft)(A1)(ft)(A1)(ft) (C4)
Notes: Award (A1)(ft) for the correct placement of \(6\).
Award (A1)(ft) for the correct placement of \(8\) and \(9\) and the empty region.
Award (A1)(ft) for the correct placement of \(2\), \(4\), \(3\), \(7\), and \(10\).
Award (A1)(ft) for the correct placement of \(1\) and \(5\).
If an element is in more than one region, award (A0) for that element.
Follow through from their answers to parts (a) and (b).
[4 marks]
Examiners report
This question was done well by most candidates. The most frequent error was to omit the placement of 1 and 5 or to include 0 in the set of even integers.
This question was done well by most candidates. The most frequent error was to omit the placement of 1 and 5 or to include 0 in the set of even integers.
This question was done well by most candidates. The most frequent error was to omit the placement of 1 and 5 or to include 0 in the set of even integers.

