| Date | November 2013 | Marks available | 1 | Reference code | 13N.2.sl.TZ0.3 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Write down | Question number | 3 | Adapted from | N/A |
Question
A group of \(120\) women in the USA were asked whether they had visited the continents of Europe (\(E\)) or South America (\(S\)) or Asia (\(A\)).
\(7\) had visited all three continents
\(28\) had visited Europe only
\(22\) had visited South America only
\(16\) had visited Asia only
\(15\) had visited Europe and South America but had not visited Asia
\(x\) had visited South America and Asia but had not visited Europe
\(2x\) had visited Europe and Asia but had not visited South America
\(20\) had not visited any of these continents
Draw a Venn diagram, using sets labelled \(E\), \(S\) and \(A\), to show this information.
Calculate the value of \(x\).
Explain, in words, the meaning of \((E \cup S) \cap A'\).
Write down \(n\left( {(E \cup S \cup A)'} \right)\).
Find the probability that a woman selected at random from the group had visited Europe.
Find the probability that a woman selected at random from the group had visited Europe, given that she had visited Asia.
Two women from the group are selected at random.
Find the probability that both women selected had visited South America.
Markscheme
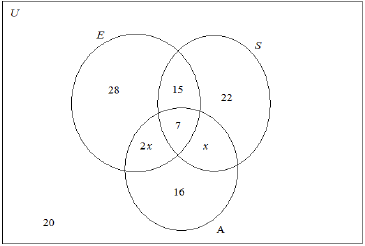 (A1)(A1)(A1)(A1)(A1)
(A1)(A1)(A1)(A1)(A1)
Notes: Award (A1) for rectangle and three labelled intersecting circles.
Award (A1) for \(7\) in correct place.
Award (A1) for \(28\), \(22\) and \(16\) in the correct places.
Award (A1) for \(15\), \(x\) and \(2x\) in the correct places.
Award (A1) for \(20\) in the correct place.
Accept \(4\) and \(8\) instead of \(x\) and \(2x\).
Do not penalize if \(U\) is omitted from the diagram.
[5 marks]
\(3x = 120 - (20 + 28 + 15 + 22 + 7 + 16)\) (M1)
Note: Award (M1) for setting up a correct equation involving \(x\), the \(120\) and values from their diagram.
\(x = 4\) (A1)(ft)(G2)
Note: Follow through from part (a). For the follow through to be awarded \(x\) must be a positive integer.
[2 marks]
(Women who had visited) Europe or South America and (but had) not (visited) Asia (A1)(A1)
Notes: Award (A1) for “(visited) Europe or South America” (or both).
Award (A1) for “and (but) had not visited Asia”.
\(E\)(urope) union \(S\)(outh America) intersected with not \(A\)(sia) earns no marks, (A0).
[2 marks]
\(20\) (A1)
Note: Award (A0) for the embedded answer of \(n(20)\).
[1 mark]
\(\frac{{58}}{{120}}{\text{ }}\left( {\frac{{29}}{{60}},{\text{ 0.483, 48.3% }}} \right){\text{ (0.48333}} \ldots {\text{)}}\) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for numerator, follow through from their value of \(x\), or their diagram, (A1) for denominator.
[2 marks]
\(\frac{{15}}{{35}}{\text{ }}\left( {\frac{3}{7},{\text{ 0.429, 42.9% }}} \right){\text{ (0.428571}} \ldots {\text{)}}\) (A1)(ft)(A1)(ft)(G2)
Note: Award (A1)(ft) for numerator, (A1)(ft) for denominator, follow through from their value of \(x\) or their diagram.
[2 marks]
\(\frac{{48}}{{120}} \times \frac{{47}}{{119}}\) (A1)(ft)(M1)
Notes: Award (A1)(ft) for two correct fractions, follow through from their denominator in part (e), follow through the numerator from their answer to part (b) or from their diagram, (M1) for multiplication of their two fractions.
\( = \frac{{2256}}{{14\,280}}\left( {\frac{{94}}{{595}},{\text{ 0.158, 15,8% }}} \right){\text{ (0.157983}} \ldots {\text{)}}\) (A1)(ft)(G2)
Notes: Award (A1)(M1)(A1) for correct fractions, correctly multiplied together with an answer of \(0.16\).
Award (A0)(M1)(A0) for \(\frac{{48}}{{120}} \times \frac{{48}}{{120}} = 0.16\).
Award (G1) for an answer of \(0.16\) with no working seen.
[3 marks]
Examiners report
Candidates seemed to be well-drilled in the technique of creating Venn diagrams and using the data from their diagrams to solve problems in probability and this question was well answered. Except for the odd mistake in determining the value of x in part (b), many candidates scored full marks on the first two parts of the question. Indeed, those who calculated an incorrect value of x were able to recover many of the marks in the remainder of the question with the use of follow through marks. ‘Explain in words…’ required candidates to answer part (c) in the context of the question so ‘E union S intersection not A’ earned no marks. Of those candidates who did answer in context, many scored 1 mark for ‘had not visited Asia’ but a significant number used ‘and’ rather than ‘or’ and consequently were not awarded the other mark for expressing \(E \cup S\) in words. Whilst many correct answers of 20 were seen for part (d), a significant number of candidates wrote down the incorrect value of 113 which presumably was arrived at by evaluating \(n((E \cap S \cap A)')\) rather than the actual demand of the question. Having a Venn diagram seemed to be a good aid for parts (e) and (f) and much good work was seen in these two parts. However, in part (g), a significant number of candidates either chose a “with replacement” method or simply did not know what to do with the probabilities once they were found. As a consequence, this part of the question proved to be quite a discriminator.
Candidates seemed to be well-drilled in the technique of creating Venn diagrams and using the data from their diagrams to solve problems in probability and this question was well answered. Except for the odd mistake in determining the value of x in part (b), many candidates scored full marks on the first two parts of the question. Indeed, those who calculated an incorrect value of x were able to recover many of the marks in the remainder of the question with the use of follow through marks. ‘Explain in words…’ required candidates to answer part (c) in the context of the question so ‘E union S intersection not A’ earned no marks. Of those candidates who did answer in context, many scored 1 mark for ‘had not visited Asia’ but a significant number used ‘and’ rather than ‘or’ and consequently were not awarded the other mark for expressing \(E \cup S\) in words. Whilst many correct answers of 20 were seen for part (d), a significant number of candidates wrote down the incorrect value of 113 which presumably was arrived at by evaluating \(n((E \cap S \cap A)')\) rather than the actual demand of the question. Having a Venn diagram seemed to be a good aid for parts (e) and (f) and much good work was seen in these two parts. However, in part (g), a significant number of candidates either chose a “with replacement” method or simply did not know what to do with the probabilities once they were found. As a consequence, this part of the question proved to be quite a discriminator.
Candidates seemed to be well-drilled in the technique of creating Venn diagrams and using the data from their diagrams to solve problems in probability and this question was well answered. Except for the odd mistake in determining the value of x in part (b), many candidates scored full marks on the first two parts of the question. Indeed, those who calculated an incorrect value of x were able to recover many of the marks in the remainder of the question with the use of follow through marks. ‘Explain in words…’ required candidates to answer part (c) in the context of the question so ‘E union S intersection not A’ earned no marks. Of those candidates who did answer in context, many scored 1 mark for ‘had not visited Asia’ but a significant number used ‘and’ rather than ‘or’ and consequently were not awarded the other mark for expressing \(E \cup S\) in words. Whilst many correct answers of 20 were seen for part (d), a significant number of candidates wrote down the incorrect value of 113 which presumably was arrived at by evaluating \(n((E \cap S \cap A)')\) rather than the actual demand of the question. Having a Venn diagram seemed to be a good aid for parts (e) and (f) and much good work was seen in these two parts. However, in part (g), a significant number of candidates either chose a “with replacement” method or simply did not know what to do with the probabilities once they were found. As a consequence, this part of the question proved to be quite a discriminator.
Candidates seemed to be well-drilled in the technique of creating Venn diagrams and using the data from their diagrams to solve problems in probability and this question was well answered. Except for the odd mistake in determining the value of x in part (b), many candidates scored full marks on the first two parts of the question. Indeed, those who calculated an incorrect value of x were able to recover many of the marks in the remainder of the question with the use of follow through marks. ‘Explain in words…’ required candidates to answer part (c) in the context of the question so ‘E union S intersection not A’ earned no marks. Of those candidates who did answer in context, many scored 1 mark for ‘had not visited Asia’ but a significant number used ‘and’ rather than ‘or’ and consequently were not awarded the other mark for expressing \(E \cup S\) in words. Whilst many correct answers of 20 were seen for part (d), a significant number of candidates wrote down the incorrect value of 113 which presumably was arrived at by evaluating \(n((E \cap S \cap A)')\) rather than the actual demand of the question. Having a Venn diagram seemed to be a good aid for parts (e) and (f) and much good work was seen in these two parts. However, in part (g), a significant number of candidates either chose a “with replacement” method or simply did not know what to do with the probabilities once they were found. As a consequence, this part of the question proved to be quite a discriminator.
Candidates seemed to be well-drilled in the technique of creating Venn diagrams and using the data from their diagrams to solve problems in probability and this question was well answered. Except for the odd mistake in determining the value of x in part (b), many candidates scored full marks on the first two parts of the question. Indeed, those who calculated an incorrect value of x were able to recover many of the marks in the remainder of the question with the use of follow through marks. ‘Explain in words…’ required candidates to answer part (c) in the context of the question so ‘E union S intersection not A’ earned no marks. Of those candidates who did answer in context, many scored 1 mark for ‘had not visited Asia’ but a significant number used ‘and’ rather than ‘or’ and consequently were not awarded the other mark for expressing \(E \cup S\) in words. Whilst many correct answers of 20 were seen for part (d), a significant number of candidates wrote down the incorrect value of 113 which presumably was arrived at by evaluating \(n((E \cap S \cap A)')\) rather than the actual demand of the question. Having a Venn diagram seemed to be a good aid for parts (e) and (f) and much good work was seen in these two parts. However, in part (g), a significant number of candidates either chose a “with replacement” method or simply did not know what to do with the probabilities once they were found. As a consequence, this part of the question proved to be quite a discriminator.
Candidates seemed to be well-drilled in the technique of creating Venn diagrams and using the data from their diagrams to solve problems in probability and this question was well answered. Except for the odd mistake in determining the value of x in part (b), many candidates scored full marks on the first two parts of the question. Indeed, those who calculated an incorrect value of x were able to recover many of the marks in the remainder of the question with the use of follow through marks. ‘Explain in words…’ required candidates to answer part (c) in the context of the question so ‘E union S intersection not A’ earned no marks. Of those candidates who did answer in context, many scored 1 mark for ‘had not visited Asia’ but a significant number used ‘and’ rather than ‘or’ and consequently were not awarded the other mark for expressing \(E \cup S\) in words. Whilst many correct answers of 20 were seen for part (d), a significant number of candidates wrote down the incorrect value of 113 which presumably was arrived at by evaluating \(n((E \cap S \cap A)')\) rather than the actual demand of the question. Having a Venn diagram seemed to be a good aid for parts (e) and (f) and much good work was seen in these two parts. However, in part (g), a significant number of candidates either chose a “with replacement” method or simply did not know what to do with the probabilities once they were found. As a consequence, this part of the question proved to be quite a discriminator.
Candidates seemed to be well-drilled in the technique of creating Venn diagrams and using the data from their diagrams to solve problems in probability and this question was well answered. Except for the odd mistake in determining the value of x in part (b), many candidates scored full marks on the first two parts of the question. Indeed, those who calculated an incorrect value of x were able to recover many of the marks in the remainder of the question with the use of follow through marks. ‘Explain in words…’ required candidates to answer part (c) in the context of the question so ‘E union S intersection not A’ earned no marks. Of those candidates who did answer in context, many scored 1 mark for ‘had not visited Asia’ but a significant number used ‘and’ rather than ‘or’ and consequently were not awarded the other mark for expressing \(E \cup S\) in words. Whilst many correct answers of 20 were seen for part (d), a significant number of candidates wrote down the incorrect value of 113 which presumably was arrived at by evaluating \(n((E \cap S \cap A)')\) rather than the actual demand of the question. Having a Venn diagram seemed to be a good aid for parts (e) and (f) and much good work was seen in these two parts. However, in part (g), a significant number of candidates either chose a “with replacement” method or simply did not know what to do with the probabilities once they were found. As a consequence, this part of the question proved to be quite a discriminator.

