| Date | May 2015 | Marks available | 2 | Reference code | 15M.1.sl.TZ1.8 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 8 | Adapted from | N/A |
Question
Aleph has an unbiased cubical (six faced) die on which are written the numbers
1 , 2 , 3 , 4 , 5 and 6.
Beth has an unbiased tetrahedral (four faced) die on which are written the numbers
2 , 3 , 5 and 7.
Complete the Venn diagram with the numbers written on Aleph’s die (\(A\)) and Beth’s die (\(B\)).
Find \(n(B \cap A')\).
Aleph and Beth are each going to roll their die once only. Shin says the probability that each die will show the same number is \(\frac{1}{8}\).
Determine whether Shin is correct. Give a reason.
Markscheme
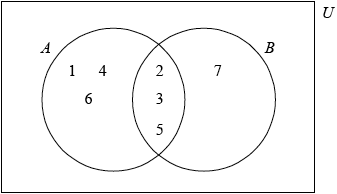 (A1)(A1) (C2)
(A1)(A1) (C2)
Note: Award (A1) for 2, 3, 5 in intersection, (A1) for 1, 4, 6, 7 correctly placed.
\(1\) (M1)(A1)(ft) (C2)
Notes: Award (M1)(A0) for listing the elements of their set \(B \cap A'\);shading the correct region on diagram; or an answer of \(1/7\) with a correct Venn diagram. Follow through from part (a).
Correct, from \((2,{\text{ }}2){\text{ }}(3,{\text{ }}3)\) and \((5,{\text{ }}5)\) on sample space
OR
Correct, from a labelled tree diagram
OR
Correct, from a sample space diagram
OR
Correct, from \(3 \times \frac{1}{4} \times \frac{1}{6}\;\;\;\)(or equivalent) (A1)(ft)(R1) (C2)
Notes: Do not award (A1)(ft)(R0). Award (R1) for a consistent reason with their part (a). Follow through from part (a).
Examiners report
The Venn diagram in part (a) was successfully completed by the majority of candidates.
Many identified correctly the set B ∩ A′ , but listed the element instead of writing the number of elements in the set.
In part (c) the majority stated that Shin was incorrect giving probabilities of 3/8 (3/6 × 3/4) or 3/7 as being the correct probability. The few candidates using a sample space diagram usually answered correctly, tree diagrams were hardly used. Many candidates did not realize that it was not enough for each to roll one of the three numbers in the intersection, but that they needed to roll the same number. Probabilities of joined events seemed to be too difficult for the majority.

