| Date | November 2014 | Marks available | 4 | Reference code | 14N.1.sl.TZ0.2 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Calculate | Question number | 2 | Adapted from | N/A |
Question
The four points A(−6, −11) , B(−2, 7) , C(4, 9) and D(6, 3) define the vertices of a kite.
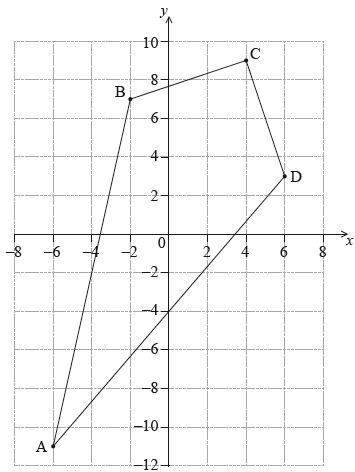
Calculate the distance between points \({\text{B}}\) and \({\text{D}}\).
The distance between points \({\text{A}}\) and \({\text{C}}\) is \(\sqrt {500} \).
Calculate the area of the kite \({\text{ABCD}}\).
Markscheme
\({\text{BD}} = \sqrt {\left( {{4^2} + {8^2}} \right)} \) (M1)
Note: Award (M1) for correct substitution into the distance formula.
\( = 8.94\left( {8.94427 \ldots ,{\text{ }}\sqrt {80} ,{\text{ }}4\sqrt 5 } \right)\) (A1) (C2)
Area \({\text{ABCD}} = 2 \times \left( {0.5 \times \frac{{{\text{their BD}}}}{2} \times \sqrt {500} } \right)\) (M1)(M1)(M1)
Note: Award (M1) for dividing their BD by 2, (M1) for correct substitution into the area of triangle formula, (M1) for adding two triangles (or multiplied by 2).
Accept alternative methods:
Area of kite \( = 0.5 \times \sqrt {500} \times \) their part (a).
Award (M1) for stating kite formula.
Award (M1) for correctly substituting in \(\sqrt {500} \).
Award (M1) for correctly substituting in their part (a).
\( = 100\) (A1) (C4)
Note: Accept 99.9522 if 3 sf answer is used from part (a).

