| Date | May 2015 | Marks available | 1 | Reference code | 15M.1.sl.TZ2.8 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Write down | Question number | 8 | Adapted from | N/A |
Question
The diagram shows a triangle \({\rm{ABC}}\). The size of angle \({\rm{C\hat AB}}\) is \(55^\circ\) and the length of \({\rm{AM}}\) is \(10\) m, where \({\rm{M}}\) is the midpoint of \({\rm{AB}}\). Triangle \({\rm{CMB}}\) is isosceles with \({\text{CM}} = {\text{MB}}\).
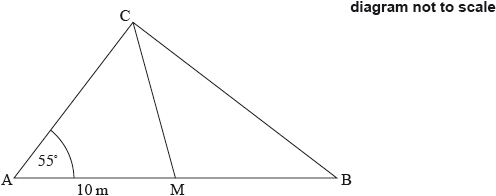
Write down the length of \({\rm{MB}}\).
Find the size of angle \({\rm{C\hat MB}}\).
Find the length of \({\rm{CB}}\).
Markscheme
\(10\) m (A1)(C1)
\({\rm{A\hat MC}} = 70^\circ \;\;\;\)OR\(\;\;\;{\rm{A\hat CM}} = 55^\circ \) (A1)
\({\rm{C\hat MB}} = 110^\circ \) (A1) (C2)
\({\text{C}}{{\text{B}}^2} = {10^2} + {10^2} - 2 \times 10 \times 10 \times \cos 110^\circ \) (M1)(A1)(ft)
Notes: Award (M1) for substitution into the cosine rule formula, (A1)(ft) for correct substitution. Follow through from their answer to part (b).
OR
\(\frac{{{\text{CB}}}}{{\sin 110^\circ }} = \frac{{10}}{{\sin 35^\circ }}\) (M1)(A1)(ft)
Notes: Award (M1) for substitution into the sine rule formula, (A1)(ft) for correct substitution. Follow through from their answer to part (b).
OR
\({\rm{A\hat CB}} = 90^\circ \) (A1)
\(\sin 55^\circ = \frac{{{\text{CB}}}}{{55}}\;\;\;\)OR\(\;\;\;\cos 35^\circ = \frac{{{\text{CB}}}}{{20}}\) (M1)
Note: Award (A1) for some indication that \({\rm{A\hat CB}} = 90^\circ \), (M1) for correct trigonometric equation.
OR
Perpendicular \({\rm{MN}}\) is drawn from \({\rm{M}}\) to \({\rm{CB}}\). (A1)
\(\frac{{\frac{1}{2}{\text{CB}}}}{{10}} = \cos 35^\circ \) (M1)
Note: Award (A1) for some indication of the perpendicular bisector of \({\rm{BC}}\), (M1) for correct trigonometric equation.
\({\text{CB}} = 16.4{\text{ (m)}}\;\;\;\left( {16.3830 \ldots {\text{ (m)}}} \right)\) (A1)(ft)(C3)
Notes: Where a candidate uses \({\rm{C\hat MB}} = 90^\circ \) and finds \({\text{CB}} = 14.1{\text{ (m)}}\) award, at most, (M1)(A1)(A0).
Where a candidate uses \({\rm{C\hat MB}} = 60^\circ \) and finds \({\text{CB}} = 10{\text{ (m)}}\) award, at most, (M1)(A1)(A0).

