| Date | May 2011 | Marks available | 2 | Reference code | 11M.1.sl.TZ2.3 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
The following diagram shows quadrilateral ABCD, with \(\overrightarrow {{\rm{AD}}} = \overrightarrow {{\rm{BC}}} \) , \(\overrightarrow {{\rm{AB}}} = \left( \begin{array}{l}
3\\
1
\end{array} \right)\) , and \(\overrightarrow {{\rm{AC}}} = \left( \begin{array}{l}
4\\
4
\end{array} \right)\) .
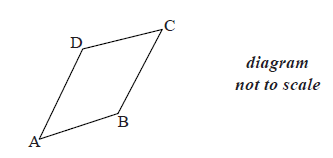
Find \(\overrightarrow {{\rm{BC}}} \) .
Show that \(\overrightarrow {{\rm{BD}}} = \left( {\begin{array}{*{20}{c}}
{ - 2}\\
2
\end{array}} \right)\) .
Show that vectors \(\overrightarrow {{\rm{BD}}} \) and \(\overrightarrow {{\rm{AC}}} \) are perpendicular.
Markscheme
evidence of appropriate approach (M1)
e.g. \(\overrightarrow {{\rm{AC}}} - \overrightarrow {{\rm{AB}}} \) , \(\left( \begin{array}{l}
4 - 3\\
4 - 1
\end{array} \right)\)
\(\overrightarrow {{\rm{BC}}} = \left( \begin{array}{l}
1\\
3
\end{array} \right)\) A1 N2
[2 marks]
METHOD 1
\(\overrightarrow {{\rm{AD}}} = \left( {\begin{array}{*{20}{c}}
1\\
3
\end{array}} \right)\) (A1)
correct approach A1
e.g. \(\overrightarrow {{\rm{AD}}} - \overrightarrow {{\rm{AB}}} \) , \(\left( \begin{array}{l}
1 - 3\\
3 - 1
\end{array} \right)\)
\(\overrightarrow {{\rm{BD}}} = \left( {\begin{array}{*{20}{c}}
{ - 2}\\
2
\end{array}} \right)\) AG N0
METHOD 2
recognizing \(\overrightarrow {{\rm{CD}}} = \overrightarrow {{\rm{BA}}} \) (A1)
correct approach A1
e.g. \(\overrightarrow {{\rm{BC}}} + \overrightarrow {{\rm{CD}}} \) , \(\left( \begin{array}{l}
1 - 3\\
3 - 1
\end{array} \right)\)
\(\overrightarrow {{\rm{BD}}} = \left( {\begin{array}{*{20}{c}}
{ - 2}\\
2
\end{array}} \right)\) AG N0
[2 marks]
METHOD 1
evidence of scalar product (M1)
e.g. \(\overrightarrow {{\rm{BD}}} \bullet \overrightarrow {{\rm{AC}}} \) , \(\left( {\begin{array}{*{20}{c}}
{ - 2}\\
2
\end{array}} \right) \bullet \left( \begin{array}{l}
4\\
4
\end{array} \right)\)
correct substitution A1
e.g. \(( - 2)(4) + (2)(4)\) , \( - 8 + 8\)
\(\overrightarrow {{\rm{BD}}} \bullet \overrightarrow {{\rm{AC}}} = 0\) A1
therefore vectors \(\overrightarrow {{\rm{BD}}} \) and \(\overrightarrow {{\rm{AC}}} \) are perpendicular AG N0
METHOD 2
attempt to find angle between two vectors (M1)
e.g. \(\frac{{{\boldsymbol{a}} \bullet {\boldsymbol{b}}}}{{{\boldsymbol{ab}}}}\)
correct substitution A1
e.g. \(\frac{{( - 2)(4) + (2)(4)}}{{\sqrt 8 \sqrt {32} }}\) , \(\cos \theta = 0\)
\(\theta = {90^ \circ }\) A1
therefore vectors \(\overrightarrow {{\rm{BD}}} \) and \(\overrightarrow {{\rm{AC}}} \) are perpendicular AG N0
[3 marks]
Examiners report
This question on two-dimensional vectors was generally very well done.
This question on two-dimensional vectors was generally very well done. A very small number of candidates had trouble with the "show that" in part (b) of the question.
Nearly all candidates knew to use the scalar product in part (c) to show that the vectors are perpendicular.

