| Date | November 2008 | Marks available | 1 | Reference code | 08N.1.sl.TZ0.4 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Write down | Question number | 4 | Adapted from | N/A |
Question
Let f be the function given by \(f(x) = {{\rm{e}}^{0.5x}}\) , \(0 \le x \le 3.5\) . The diagram shows the graph of f .
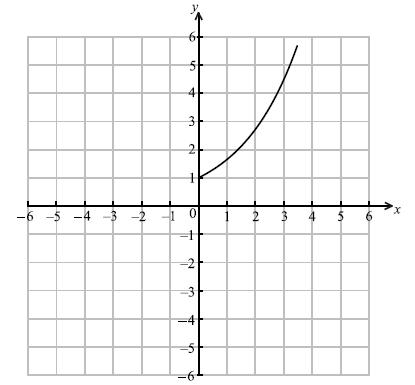
On the same diagram, sketch the graph of \({f^{ - 1}}\) .
Write down the range of \({f^{ - 1}}\) .
Find \({f^{ - 1}}(x)\) .
Markscheme
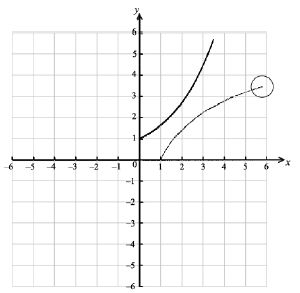 A1A1A1 N3
A1A1A1 N3
Note: Award A1 for approximately correct (reflected) shape, A1 for right end point in circle, A1 for through \((1{\text{, }}0)\) .
\(0 \le y \le 3.5\) A1 N1
[1 mark]
interchanging x and y (seen anywhere) M1
e.g. \(x = {e^{0.5y}}\)
evidence of changing to log form A1
e.g. \(\ln x = 0.5y\) , \(\ln x = \ln {{\rm{e}}^{0.5y}}\) (any base), \(\ln x = 0.5y\ln {\rm{e}}\) (any base)
\({f^{ - 1}}(x) = 2\ln x\) A1 N1
[3 marks]
Examiners report
There were a large number of candidates who were unaware of the geometric relationship between a function and its inverse. Those that had some idea of the shape of the graph often did not consider the specified domain. Many more students were able to use an analytical approach to finding the inverse of a function and had little problem using logarithms to solve for y. Candidates were clearly more comfortable with algebraic procedures than graphical interpretations.
There were a large number of candidates who were unaware of the geometric relationship between a function and its inverse. Those that had some idea of the shape of the graph often did not consider the specified domain. Many more students were able to use an analytical approach to finding the inverse of a function and had little problem using logarithms to solve for y. Candidates were clearly more comfortable with algebraic procedures than graphical interpretations.
There were a large number of candidates who were unaware of the geometric relationship between a function and its inverse. Those that had some idea of the shape of the graph often did not consider the specified domain. Many more students were able to use an analytical approach to finding the inverse of a function and had little problem using logarithms to solve for y. Candidates were clearly more comfortable with algebraic procedures than graphical interpretations.

