IB Questionbank

Processing math: 100%

Updates to Questionbank

User interface language: English | Español

Date	May 2017	Marks available	2	Reference code	17M.2.sl.TZ2.3
Level	SL only	Paper	2	Time zone	TZ2
Command term	Write down	Question number	3	Adapted from	N/A

Question

The following diagram shows the graph of a function $y = f(x)$ , for $- 6 \leqslant x \leqslant - 2$ .

The points $( - 6,{\text{ }}6)$ and $( - 2,{\text{ }}6)$ lie on the graph of $f$ . There is a minimum point at $( - 4,{\text{ }}0)$ .

Let $g(x) = f(x - 5)$ .

Write down the range of $f$ .

[2]

a.

On the grid above, sketch the graph of $g$ .

[2]

b.

Write down the domain of $g$ .

[2]

c.

Markscheme

correct interval A2 N2

eg $\,\,\,\,\,$ $0 \leqslant y \leqslant 6,{\text{ }}[0,{\text{ }}6]$ , from 0 to 6

[2 marks]

a.

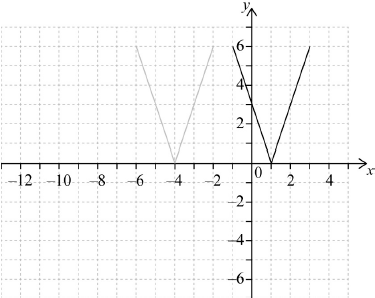M17/5/MATME/SP2/ENG/TZ2/03.b/M M1A1 N2

Note: Award M1 for a horizontal shift of the whole shape, 5 units to the left or right and A1 for the correct graph.

[2 marks]

b.

correct interval A2 N2

eg $\,\,\,\,\,$ $- 1 \leqslant x \leqslant 3,{\text{ }}[ - 1,{\text{ }}3]$ , from $- 1$ to 3

[2 marks]

c.

Examiners report

[N/A]

a.

[N/A]

b.

[N/A]

c.

Syllabus sections

Topic 2 - Functions and equations » 2.1 » Concept of function

$f:x \mapsto f\left( x \right)$ .

Show 22 related questions

17M.2.sl.TZ2.3b: On the grid above, sketch the graph of $g$ .
17M.2.sl.TZ2.3a: Write down the range of $f$ .
16M.1.sl.TZ1.1c: Find ${f^{ - 1}}(x)$ .
16M.1.sl.TZ1.1b: Find $(f \circ g)(x)$ .
16M.1.sl.TZ1.1a: Write down $g(2)$ .
08N.1.sl.TZ0.4b: Write down the range of ${f^{ - 1}}$ .
08M.1.sl.TZ2.5b(i) and (ii): Let $g(x) = f(x + 3)$ . (i) Find $g( - 3)$ . (ii) Describe fully the...
09N.1.sl.TZ0.1a: (i) Find $g(0)$ . (ii) Find $(f \circ g)(0)$ .
SPNone.2.sl.TZ0.10a(i), (ii) and (iii): Jane thinks that the function $f(t) = - 0.25{t^3} - 2.32{t^2} + 1.93t + 106$ is a suitable...
13M.1.sl.TZ1.10a: Find the value of $f(0)$ .
13M.2.sl.TZ1.9c: Find the range of $f$ .
13M.2.sl.TZ1.9a: Write down $f(0)$ .
13M.1.sl.TZ2.4a.i: Write down the value of $f(2)$ .
13M.1.sl.TZ2.10c: find the $y$ -coordinate of P.
13M.1.sl.TZ2.10a: Write down the value of $g(3)$ , of $f'(3)$ , and of $h''(2)$ .
14M.1.sl.TZ2.3a(ii): Write down the value of ${f^{ - 1}}(1)$ .
14M.1.sl.TZ2.3a(i): Write down the value of $f( - 3)$ .
14M.1.sl.TZ2.3b: Find the domain of ${f^{ - 1}}$ .
17N.1.sl.TZ0.3c: On the grid, sketch the graph of ${f^{ - 1}}$ .
17N.1.sl.TZ0.3b.ii: Write down ${f^{ - 1}}(2)$ .
17N.1.sl.TZ0.3b.i: Write down $f(2)$ ;
17N.1.sl.TZ0.3a: Write down the range of $f$ .

Hide related questions