| Date | May 2018 | Marks available | 3 | Reference code | 18M.3.AHL.TZ0.Hca_3 |
| Level | Additional Higher Level | Paper | Paper 3 | Time zone | Time zone 0 |
| Command term | Find | Question number | Hca_3 | Adapted from | N/A |
Question
Find the value of .
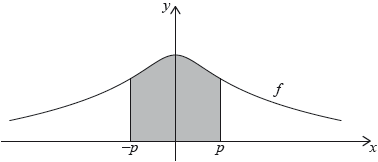
Illustrate graphically the inequality .
Hence write down a lower bound for .
Find an upper bound for .
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(A1)
Note: The above A1 for using a limit can be awarded at any stage.
Condone the use of .
Do not award this mark to candidates who use as the upper limit throughout.
= M1
A1
[3 marks]
A1A1A1A1
A1 for the curve
A1 for rectangles starting at
A1 for at least three upper rectangles
A1 for at least three lower rectangles
Note: Award A0A1 for two upper rectangles and two lower rectangles.
sum of areas of the lower rectangles < the area under the curve < the sum of the areas of the upper rectangles so
AG
[4 marks]
a lower bound is A1
Note: Allow FT from part (a).
[1 mark]
METHOD 1
(M1)
(M1)
, an upper bound A1
Note: Allow FT from part (a).
METHOD 2
changing the lower limit in the inequality in part (b) gives
(A1)
(M1)
, an upper bound A1
Note: Condone candidates who do not use a limit.
[3 marks]