IB Questionbank

User interface language: English | Español

Date	May 2017	Marks available	8	Reference code	17M.1.SL.TZ1.S_9
Level	Standard Level	Paper	Paper 1	Time zone	Time zone 1
Command term	Find	Question number	S_9	Adapted from	N/A

Question

A quadratic function $f$ can be written in the form $f(x) = a(x - p)(x - 3)$ . The graph of $f$ has axis of symmetry $x = 2.5$ and $y$ -intercept at $(0,{\text{ }} - 6)$

Find the value of $p$ .

[3]

Find the value of $a$ .

[3]

The line $y = kx - 5$ is a tangent to the curve of $f$ . Find the values of $k$ .

[8]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

METHOD 1 (using x-intercept)

determining that 3 is an $x$ -intercept (M1)

eg 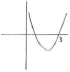$\,\,\,\,\,$ $x - 3 = 0$ , M17/5/MATME/SP1/ENG/TZ1/09.a/M

valid approach (M1)

eg $\,\,\,\,\,$ $3 - 2.5,{\text{ }}\frac{{p + 3}}{2} = 2.5$

$p = 2$ A1 N2

METHOD 2 (expanding f (x))

correct expansion (accept absence of $a$ ) (A1)

eg $\,\,\,\,\,$ $a{x^2} - a(3 + p)x + 3ap,{\text{ }}{x^2} - (3 + p)x + 3p$

valid approach involving equation of axis of symmetry (M1)

eg $\,\,\,\,\,$ $\frac{{ - b}}{{2a}} = 2.5,{\text{ }}\frac{{a(3 + p)}}{{2a}} = \frac{5}{2},{\text{ }}\frac{{3 + p}}{2} = \frac{5}{2}$

$p = 2$ A1 N2

METHOD 3 (using derivative)

correct derivative (accept absence of $a$ ) (A1)

eg $\,\,\,\,\,$ $a(2x - 3 - p),{\text{ }}2x - 3 - p$

valid approach (M1)

eg $\,\,\,\,\,$ $f’(2.5) = 0$

$p = 2$ A1 N2

[3 marks]

attempt to substitute $(0,{\text{ }} - 6)$ (M1)

eg $\,\,\,\,\,$ $- 6 = a(0 - 2)(0 - 3),{\text{ }}0 = a( - 8)( - 9),{\text{ }}a{(0)^2} - 5a(0) + 6a = - 6$

correct working (A1)

eg $\,\,\,\,\,$ $- 6 = 6a$

$a = - 1$ A1 N2

[3 marks]

METHOD 1 (using discriminant)

recognizing tangent intersects curve once (M1)

recognizing one solution when discriminant = 0 M1

attempt to set up equation (M1)

eg $\,\,\,\,\,$ $g = f,{\text{ }}kx - 5 = - {x^2} + 5x - 6$

rearranging their equation to equal zero (M1)

eg $\,\,\,\,\,$ ${x^2} - 5x + kx + 1 = 0$

correct discriminant (if seen explicitly, not just in quadratic formula) A1

eg $\,\,\,\,\,$ ${(k - 5)^2} - 4,{\text{ }}25 - 10k + {k^2} - 4$

correct working (A1)

eg $\,\,\,\,\,$ $k - 5 = \pm 2,{\text{ }}(k - 3)(k - 7) = 0,{\text{ }}\frac{{10 \pm \sqrt {100 - 4 \times 21} }}{2}$

$k = 3,{\text{ }}7$ A1A1 N0

METHOD 2 (using derivatives)

attempt to set up equation (M1)

eg $\,\,\,\,\,$ $g = f,{\text{ }}kx - 5 = - {x^2} + 5x - 6$

recognizing derivative/slope are equal (M1)

eg $\,\,\,\,\,$ $f’ = {m_T},{\text{ }}f' = k$

correct derivative of $f$ (A1)

eg $\,\,\,\,\,$ $- 2x + 5$

attempt to set up equation in terms of either $x$ or $k$ M1

eg $\,\,\,\,\,$ $( - 2x + 5)x - 5 = - {x^2} + 5x - 6,{\text{ }}k\left( {\frac{{5 - k}}{2}} \right) - 5 = - {\left( {\frac{{5 - k}}{2}} \right)^2} + 5\left( {\frac{{5 - k}}{2}} \right) - 6$

rearranging their equation to equal zero (M1)

eg $\,\,\,\,\,$ ${x^2} - 1 = 0,{\text{ }}{k^2} - 10k + 21 = 0$

correct working (A1)

eg $\,\,\,\,\,$ $x = \pm 1,{\text{ }}(k - 3)(k - 7) = 0,{\text{ }}\frac{{10 \pm \sqrt {100 - 4 \times 21} }}{2}$

$k = 3,{\text{ }}7$ A1A1 N0

[8 marks]

Examiners report

[N/A]

Syllabus sections

Topic 4—Statistics and probability » SL 4.1—Concepts, reliability and sampling techniques

Show 80 related questions

22M.2.AHL.TZ1.3a:
Name the type of sampling that best describes the method used by the Principal.
22M.2.SL.TZ1.3b:
Determine if the Netherlands’ score is an outlier for this data. Justify your answer.
19M.2.AHL.TZ1.H_3b.ii:
the standard deviation.
18N.2.AHL.TZ0.H_10b.ii:
an estimate for the standard deviation of the number of emails received per working day.
EXM.2.SL.TZ0.5d:
State an assumption that the company is making, in order to use a t-test.
EXM.2.SL.TZ0.5c.i:
The new drug.
EXM.2.SL.TZ0.5b:
Calculate the number of volunteers in the sample under the age of 30.
18N.2.AHL.TZ0.H_10d:
Suppose that the probability of Archie receiving more than 10 emails in total on any one day is 0.99. Find the value of λ.
EXM.2.SL.TZ0.5e:
State the hypotheses for this t-test.
22M.1.SL.TZ2.7a:
Show that the test score of $25$ would not be considered an outlier.
18M.1.AHL.TZ2.H_3b.i:
Find μ, the expected value of X.
18N.2.AHL.TZ0.H_10a.ii:
Using this distribution model, find the standard deviation of $X$ .
18N.2.AHL.TZ0.H_10b.i:
an estimate for the mean number of emails received per working day.
19M.2.SL.TZ1.S_9b:
Find u.
18M.1.SL.TZ1.S_2a:
Find the value of the interquartile range.
17M.1.SL.TZ1.S_6a.i:
Write down the gradient of the curve of $f$ at P.
17M.2.SL.TZ2.S_8b.i:
Write down the coordinates of A.
EXM.2.SL.TZ0.5f:
Find the p-value for this t-test.
EXM.2.SL.TZ0.5c.ii:
The current drug.
EXM.1.SL.TZ0.5c:
Give an example of a set of data with 7 numbers in it that does have an outlier, justify this fact by stating the Interquartile Range.
19M.1.SL.TZ2.S_9d:
The following diagram shows the graph of $f$ for 0 ≤ $x$ ≤ 3. Line $M$ is a tangent to the graph of $f$ at point P.

Given that $M$ is parallel to $L$ , find the $x$ -coordinate of P.
18M.1.AHL.TZ2.H_3b.ii:
Find P(X > μ).
SPM.1.SL.TZ0.3b:
Find the value of $k$ .
EXM.2.SL.TZ0.5g:
State the conclusion of this test, in context, giving a reason.
17N.1.SL.TZ0.S_5a:
Find $(g \circ f)(x)$ .
19M.2.SL.TZ1.S_9d.iii:
Hence or otherwise, find the obtuse angle formed by the tangent line to $f$ at $x = 8$ and the tangent line to $f$ at $x = 2$ .
17M.2.SL.TZ2.S_8b.ii:
Write down the rate of change of $f$ at A.
18N.2.AHL.TZ0.H_10a.i:
Using this distribution model, find ${\text{P}}\left( {X < 60} \right)$ .
18M.1.SL.TZ1.S_2b:
One student sent k text messages, where k > 11 . Given that k is an outlier, find the least value of k.
18N.2.AHL.TZ0.H_10e:
Now suppose that Archie received exactly 20 emails in total in a consecutive two day period. Show that the probability that he received exactly 10 of them on the first day is independent of λ.
19M.2.SL.TZ1.S_9d.i:
Find $\left( {f \circ f} \right)\left( x \right)$ .
17M.2.SL.TZ2.S_8c.i:
Find the coordinates of B.
18N.2.AHL.TZ0.H_10c:
Give one piece of evidence that suggests Willow’s Poisson distribution model is not a good fit.
19M.2.SL.TZ1.S_9c:
Find the acute angle between $y = x$ and $L$ .
18N.1.SL.TZ0.S_10b.ii:
Hence, find the equation of L in terms of $a$ .
18N.1.SL.TZ0.S_10a:
Find the coordinates of P.
16N.2.SL.TZ0.S_10a:
(i) Find the value of $c$ .

(ii) Show that $b = \frac{\pi }{6}$ .

(iii) Find the value of $a$ .
EXM.2.SL.TZ0.5a:
State the name for this type of sampling technique.
SPM.1.SL.TZ0.3a:
State whether the data is discrete or continuous.
17M.1.SL.TZ1.S_6b:
Determine the concavity of the graph of $f$ when $4 < x < 5$ and justify your answer.
17M.1.SL.TZ1.S_9b:
Find the value of $a$ .
16N.2.AHL.TZ0.H_11d:
(i) Hence show that $X$ has two modes ${m_1}$ and ${m_2}$ .

(ii) State the values of ${m_1}$ and ${m_2}$ .
18N.1.SL.TZ0.S_10b.i:
Find $f'\left( x \right)$ .
17M.1.SL.TZ1.S_6a.ii:
Find the equation of the normal to the curve of $f$ at P.
19M.1.SL.TZ2.S_9b:
Line $L$ passes through the origin and has a gradient of ${\text{tan}}\,\theta$ . Find the equation of $L$ .
17M.1.SL.TZ1.S_9a:
Find the value of $p$ .
19M.1.SL.TZ2.S_9a:
Find the value of ${\text{tan}}\,\theta$ .
18N.1.SL.TZ0.S_10c:
The graph of $f$ has a local minimum at the point Q. The line L passes through Q.

Find the value of $a$ .
16N.2.AHL.TZ0.H_11b:
Find the values of the constants $a$ and $b$ .
16N.2.AHL.TZ0.H_11a:
Show that ${\text{P}}(X = 3) = 0.001$ and ${\text{P}}(X = 4) = 0.0027$ .
18N.2.SL.TZ0.S_10c:
When $t$ = 0, the volume of water in the container is 2.3 m³. It is known that the container is never completely full of water during the 4 hour period.

Find the minimum volume of empty space in the container during the 4 hour period.
19M.1.SL.TZ2.S_9c:
Find the derivative of $f$ .
EXN.1.SL.TZ0.1b:
The Principal selects the students for the sample by asking those who took part in a previous survey if they would like to take part in another. She takes the first of those who reply positively, up to the maximum needed for the sample.

State which two of the sampling methods listed below best describe the method used.

Stratified Quota Convenience Systematic Simple random
16N.2.SL.TZ0.S_10b:
(i) Write down the value of $k$ .

(ii) Find $g(x)$ .
17M.2.SL.TZ2.S_8d:
Let $R$ be the region enclosed by the graph of $f$ , the $x$ -axis, the line $x = b$ and the line $x = a$ . The region $R$ is rotated 360° about the $x$ -axis. Find the volume of the solid formed.
EXM.1.SL.TZ0.5b:
Hence, show that a data set with only 5 numbers in it cannot have any outliers.
17M.2.SL.TZ2.S_8a:
Find the value of $p$ .
SPM.1.SL.TZ0.3c:
It was not possible to ask every person in the school, so the Headmaster arranged the student names in alphabetical order and then asked every 10th person on the list.

Identify the sampling technique used in the survey.
18N.2.SL.TZ0.S_10a:
Find the volume of the container.
19M.2.SL.TZ1.S_3a:
Find $f'\left( x \right)$ .
21M.2.SL.TZ1.1d:
Determine whether Jason is correct. Support your reasoning.
21M.1.AHL.TZ1.11a:
Identify the type of sampling used by the restaurant manager.
16N.2.AHL.TZ0.H_11e:
Determine the minimum value of $x$ such that the probability Kati receives at least one free gift is greater than 0.5.
18N.2.SL.TZ0.S_10b.ii:
During the interval $p$ < $t$ < $q$ , he volume of water in the container increases by $k$ m³. Find the value of $k$ .
EXM.1.SL.TZ0.5a:
Recalling definitions, such as the Lower Quartile is the $\frac{{n + 1}}{4}th$ piece of data with the data placed in order, find an expression for the Interquartile Range.
17N.1.SL.TZ0.S_5b:
Given that $\mathop {\lim }\limits_{x \to + \infty } (g \circ f)(x) = - 3$ , find the value of $b$ .
19M.2.SL.TZ1.S_9a:
Find the gradient of $L$ .
19M.2.SL.TZ1.S_3b:
The graph of $f$ has a horizontal tangent line at $x = 0$ and at $x = a$ . Find $a$ .
19M.2.SL.TZ1.S_9d.ii:
Hence, write down ${f^{ - 1}}\left( x \right)$ .
21M.2.SL.TZ1.1a:
State which of the two sampling methods, systematic or quota, Jason has used.
18M.1.AHL.TZ2.H_3a:
Find the value of p.
18N.2.SL.TZ0.S_10b.i:
Find the value of $p$ and of $q$ .
16N.2.SL.TZ0.S_10c:
(i) Find $w$ .

(ii) Hence or otherwise, find the maximum positive rate of change of $g$ .
21M.3.AHL.TZ1.2b:
Show that $11$ employees are selected for the sample from the national department.
21M.2.SL.TZ2.1a:
State the sampling method being used.
16N.2.AHL.TZ0.H_11c:
Deduce that $\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n - 1)}} = \frac{{0.9(n - 1)}}{{n - 3}}$ for $n > 3$ .
21M.3.AHL.TZ2.1b:
Juliet classifies response $K$ as an outlier and removes it from the data. Suggest one possible justification for her decision to remove it.
EXN.1.SL.TZ0.1a:
Calculate the number of grade $12$ students who should be in the sample.
17M.2.SL.TZ2.S_8c.ii:
Find the the rate of change of $f$ at B.
18M.1.SL.TZ1.S_7:
Consider f(x), g(x) and h(x), for x∈ $\mathbb{R}$ where h(x) = $\left( {f \circ g} \right)$ (x).

Given that g(3) = 7 , g′ (3) = 4 and f ′ (7) = −5 , find the gradient of the normal to the curve of h at x = 3.

Hide related questions

Topic 4—Statistics and probability

Question

Markscheme

Examiners report

Syllabus sections

View options