| Date | May 2017 | Marks available | 3 | Reference code | 17M.1.AHL.TZ1.H_12 |
| Level | Additional Higher Level | Paper | Paper 1 (without calculator) | Time zone | Time zone 1 |
| Command term | Sketch | Question number | H_12 | Adapted from | N/A |
Question
Consider the function .
Show that the graph of is concave up for .
[3]
e.i.
Sketch the graph of showing clearly any intercepts with the axes.
[3]
e.ii.
Markscheme
M1A1
for concave up R1AG
[3 marks]
e.i.
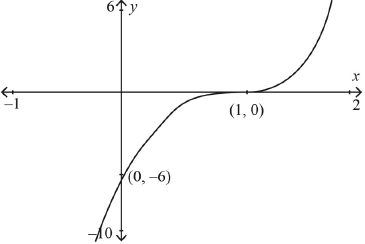
-intercept at A1
-intercept at A1
stationary point of inflexion at with correct curvature either side A1
[3 marks]
e.ii.
Examiners report
[N/A]
e.i.
[N/A]
e.ii.

