DP Physics Questionbank

Option D: Astrophysics (Core topics)
Description
Overview of the essential ideas for this topic
D.1: One of the most difficult problems in astronomy is coming to terms with the vast distances between stars and galaxies and devising accurate methods for measuring them.
D.2: A simple diagram that plots the luminosity versus the surface temperature of stars reveals unusually detailed patterns that help understand the inner workings of stars. Stars follow well-defined patterns from the moment they are created out of collapsing interstellar gas, to their lives on the main sequence and to their eventual death.
D.3: The Hot Big Bang model is a theory that describes the origin and expansion of the universe and is supported by extensive experimental evidence.
Directly related questions
-
16N.3.SL.TZ0.15e:
A standard Hertzsprung–Russell (HR) diagram is shown.
Using the HR diagram, draw the present position of Alpha Centauri A and its expected evolutionary path.
-
16N.3.SL.TZ0.15b:
(i) Calculate .
(ii) The luminosity of the Sun is 3.8 × 1026 W. Calculate the radius of Alpha Centauri A.
-
16N.3.SL.TZ0.16a:
Determine the distance from Earth to the Cepheid star in parsecs. The luminosity of the Sun is 3.8 × 1026 W. The average apparent brightness of the Cepheid star is 1.1 × 10–9 W m–2.
- 16N.3.SL.TZ0.17b: A spectral line in the hydrogen spectrum measured in the laboratory today has a wavelength of...
- 16N.3.SL.TZ0.15a: State what is meant by a binary star system.
- 16N.3.SL.TZ0.15d: Alpha Centauri A is in equilibrium at constant radius. Explain how this equilibrium is maintained.
-
16N.3.SL.TZ0.15c:
Show, without calculation, that the radius of Alpha Centauri B is smaller than the radius of Alpha Centauri A.
- 16N.3.SL.TZ0.17a: Identify two other characteristics of the CMB radiation that are predicted from the Hot Big Bang...
- 16N.3.SL.TZ0.16b: Explain why Cephids are used as standard candles.
-
17M.3.SL.TZ1.9a.iv:
Determine the distance of Theta 1 Orionis in AU.
-
17M.3.SL.TZ1.10c.ii:
Estimate the size of the Universe relative to its present size when the light was emitted by the galaxy in (c).
-
17M.3.SL.TZ1.9a.i:
State what is meant by a main sequence star.
-
17M.3.SL.TZ1.10a.i:
State two characteristics of the cosmic microwave background (CMB) radiation.
-
17M.3.SL.TZ1.10c.i:
Determine the distance to this galaxy using a value for the Hubble constant of H0 = 68 km s–1Mpc–1.
-
17M.3.SL.TZ1.10a.ii:
The present temperature of the CMB is 2.8 K. Calculate the peak wavelength of the CMB.
-
17M.3.SL.TZ1.9a.ii:
Show that the mass of Theta 1 Orionis is about 40 solar masses.
-
17M.3.SL.TZ1.9b:
Discuss how Theta 1 Orionis does not collapse under its own weight.
-
17M.3.SL.TZ1.10b:
Describe how the CMB provides evidence for the Hot Big Bang model of the universe.
-
17M.3.SL.TZ1.9a.iii:
The surface temperature of the Sun is about 6000 K. Estimate the surface temperature of Theta 1 Orionis.
-
17M.3.SL.TZ1.9c:
The Sun and Theta 1 Orionis will eventually leave the main sequence. Compare and contrast the different stages in the evolution of the two stars.
-
17M.3.SL.TZ2.11b:
The Hertzsprung–Russell (HR) diagram shows two main sequence stars X and Y and includes lines of constant radius. R is the radius of the Sun.
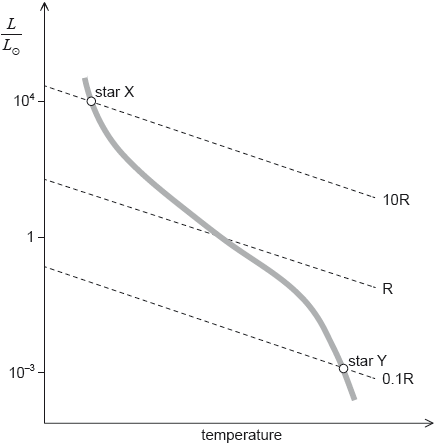
Using the mass–luminosity relation and information from the graph, determine the ratio .
-
17M.3.SL.TZ2.11c.iii:
The radius of a typical neutron star is 20 km and its surface temperature is 106 K. Determine the luminosity of this neutron star.
-
17M.3.SL.TZ2.11a:
State the most abundant element in the core and the most abundant element in the outer layer.
-
17M.3.SL.TZ2.11c.iv:
Determine the region of the electromagnetic spectrum in which the neutron star in (c)(iii) emits most of its energy.
-
17M.3.SL.TZ2.12b:
State two features of the cosmic microwave background (CMB) radiation which are consistent with the Big Bang model.
-
17M.3.SL.TZ2.12a:
Describe what is meant by the Big Bang model of the universe.
-
17M.3.SL.TZ2.11c.ii:
Outline why the neutron star that is left after the supernova stage does not collapse under the action of gravitation.
-
17M.3.SL.TZ2.11c.i:
On the HR diagram in (b), draw a line to indicate the evolutionary path of star X.
-
17M.3.SL.TZ2.12c.ii:
Describe how type Ia supernovae could be used to measure the distance to this galaxy.
-
17M.3.SL.TZ2.12c.i:
Determine the distance to the galaxy in Mpc.
-
20N.3.SL.TZ0.17a:
Show by calculation that Eta Aquilae A is not on the main sequence.
- 20N.3.SL.TZ0.17d: Eta Aquilae A is a Cepheid variable. Explain why the brightness of Eta Aquilae A varies.
-
20N.3.SL.TZ0.16b:
Outline how Hubble’s law is related to .
- 20N.3.SL.TZ0.14b(i): Comets develop a tail as they approach the Sun. Identify one other characteristic of comets.
-
20N.3.SL.TZ0.15a:
Show that the apparent brightness , where is the distance of the object from Earth, is the surface temperature of the object and is the surface area of the object.
-
20N.3.SL.TZ0.16a:
The light from a distant galaxy shows that .
Calculate the ratio .
-
20N.3.SL.TZ0.14a:
The astronomical unit () and light year () are convenient measures of distance in astrophysics. Define each unit.
:
:
-
20N.3.SL.TZ0.15b:
Two of the brightest objects in the night sky seen from Earth are the planet Venus and the star Sirius. Explain why the equation is applicable to Sirius but not to Venus.
-
20N.3.SL.TZ0.17b(i):
Estimate, in , the distance to Eta Aquilae A using the parallax angle in the table.
-
20N.3.HL.TZ0.21b:
Outline how Hubble’s law is related to .
- 20N.3.SL.TZ0.14b(ii): Identify one object visible in the image that is outside our Solar System.
- 20N.3.HL.TZ0.22d: Eta Aquilae A is a Cepheid variable. Explain why the brightness of Eta Aquilae A varies.
-
20N.3.SL.TZ0.17b(ii):
Estimate, in , the distance to Eta Aquilae A using the luminosity in the table, given that .
-
20N.3.HL.TZ0.22b(ii):
Estimate, in , the distance to Eta Aquilae A using the luminosity in the table, given that .
-
20N.3.HL.TZ0.22b(i):
Estimate, in , the distance to Eta Aquilae A using the parallax angle in the table.
-
20N.3.HL.TZ0.21a:
The light from a distant galaxy shows that .
Calculate the ratio .
-
20N.3.HL.TZ0.22a:
Show by calculation that Eta Aquilae A is not on the main sequence.
-
17N.3.SL.TZ0.13b:
Determine the velocity of the galaxy relative to Earth.
-
17N.3.SL.TZ0.12d.i:
Determine the radius of Sirius B in terms of the radius of the Sun.
- 17N.3.SL.TZ0.12d.ii: Identify the star type of Sirius B.
- 17N.3.SL.TZ0.12e.i: draw the approximate positions of Sirius A, labelled A and Sirius B, labelled B.
- 17N.3.SL.TZ0.12e.ii: sketch the expected evolutionary path for Sirius A.
- 17N.3.SL.TZ0.13a: Outline one reason for the difference in wavelength.
-
18M.3.SL.TZ2.11d.ii:
plot the position, using the letter P, of the main sequence star P you calculated in (b).
-
18M.3.SL.TZ2.11d.iii:
plot the position, using the letter G, of Gacrux.
-
18M.3.SL.TZ2.11c.i:
The luminosity of the Sun L is 3.85 × 1026 W. Determine the luminosity of Gacrux relative to the Sun.
-
18M.3.SL.TZ2.11c.ii:
The distance to Gacrux can be determined using stellar parallax. Outline why this method is not suitable for all stars.
-
18M.3.SL.TZ2.12a:
Estimate, using the data, the age of the universe. Give your answer in seconds.
-
18M.3.SL.TZ2.11a:
Main sequence stars are in equilibrium under the action of forces. Outline how this equilibrium is achieved.
-
18M.3.SL.TZ2.11e:
Discuss, with reference to its change in mass, the evolution of star P from the main sequence until its final stable phase.
-
18M.3.SL.TZ2.11b:
A main sequence star P, is 1.3 times the mass of the Sun. Calculate the luminosity of P relative to the Sun.
-
18M.3.SL.TZ2.11d.i:
draw the main sequence.
-
18M.3.SL.TZ2.12b:
Identify the assumption that you made in your answer to (a).
-
18M.3.SL.TZ2.12c:
On the graph, one galaxy is labelled A. Determine the size of the universe, relative to its present size, when light from the galaxy labelled A was emitted.
-
18M.3.SL.TZ1.10a.i:
Distinguish between the solar system and a galaxy.
-
18M.3.SL.TZ1.10a.ii:
Distinguish between a planet and a comet.
-
18M.3.SL.TZ1.11a.i:
Suggest, using the graphs, why star X is most likely to be a main sequence star.
-
18M.3.SL.TZ1.11a.ii:
Show that the temperature of star X is approximately 10 000 K.
-
18M.3.SL.TZ1.11b.i:
Write down the luminosity of star X (LX) in terms of the luminosity of the Sun (Ls).
-
18M.3.SL.TZ1.11b.ii:
Determine the radius of star X (RX) in terms of the radius of the Sun (Rs).
-
18M.3.SL.TZ1.11b.iii:
Estimate the mass of star X (MX) in terms of the mass of the Sun (Ms).
-
18M.3.SL.TZ1.11c:
Star X is likely to evolve into a stable white dwarf star.
Outline why the radius of a white dwarf star reaches a stable value.
-
18M.3.SL.TZ1.12a:
Explain how international collaboration has helped to refine this value.
-
18M.3.SL.TZ1.12b:
Estimate, in Mpc, the distance between the galaxy and the Earth.
- 21N.1.SL.TZ0.30: Which is correct for a black-body radiator? A. The power it emits from a unit surface area...
- 18N.3.SL.TZ0.12d: Describe the stages in the evolution of Epsilon Indi from the point when it leaves the main...
-
18N.3.SL.TZ0.12b:
Epsilon Indi is a main sequence star. Show that the mass of Epsilon Indi is 0.64 .
- 18N.3.SL.TZ0.12a.ii: Using the axis, draw the variation with wavelength of the intensity of the radiation emitted by...
-
18N.3.HL.TZ0.18a.i:
Determine the peak wavelength of the radiation emitted by Epsilon Indi.
- 18N.3.SL.TZ0.12c: Describe how the chemical composition of a star may be determined.
-
18N.3.HL.TZ0.19b:
Use the graph to determine the age of the universe in s.
- 18N.3.SL.TZ0.11a: Distinguish between a constellation and an open cluster.
-
18N.3.SL.TZ0.13a:
Outline how Hubble measured the recessional velocities of galaxies.
- 18N.3.SL.TZ0.11b.ii: State why there is a maximum distance that astronomers can measure using stellar parallax.
-
18N.3.SL.TZ0.12a.iii:
The following data are available for the Sun.
Surface temperature = 5800 K
Luminosity =
Mass =
Radius =
Epsilon Indi has a radius of 0.73 . Show that the luminosity of Epsilon Indi is 0.2 .
- 18N.3.SL.TZ0.11b.i: The parallax angle of Mintaka measured from Earth is 3.64 × 10–3 arc-second. Calculate, in...
-
18N.3.SL.TZ0.12a.i:
Determine the peak wavelength of the radiation emitted by Epsilon Indi.
-
18N.3.SL.TZ0.13b:
Using the graph, determine in s, the age of the universe.
- 18N.3.HL.TZ0.17b.ii: State why there is a maximum distance that astronomers can measure using stellar parallax.
- 18N.3.HL.TZ0.17b.i: The parallax angle of Mintaka measured from Earth is 3.64 × 10–3 arc-second. Calculate, in...
-
18N.3.HL.TZ0.19a:
Outline how Hubble measured the recessional velocities of galaxies.
- 18N.3.HL.TZ0.17a: Distinguish between a constellation and an open cluster.
-
18N.3.HL.TZ0.18b:
Epsilon Indi is a main sequence star. Show that the mass of Epsilon Indi is 0.64 .
-
18N.3.HL.TZ0.18a.iii:
The following data are available for the Sun.
Surface temperature = 5800 K
Luminosity =
Mass =
Radius =
Epsilon Indi has a radius of 0.73 . Show that the luminosity of Epsilon Indi is 0.2 .
- 18N.3.HL.TZ0.18a.ii: Using the axis, draw the variation with wavelength of the intensity of the radiation emitted by...
- 18N.3.HL.TZ0.18d: Describe the stages in the evolution of Epsilon Indi from the point when it leaves the main...
-
18N.3.HL.TZ0.18c:
The Sun will spend about nine billion years on the main sequence. Calculate how long Epsilon Indi will spend on the main sequence.
- 19M.3.SL.TZ2.14ai: A galaxy is 1.6 × 108 ly from Earth. Show that its recessional speed as measured from Earth is...
- 19M.3.SL.TZ2.13aii: Explain how Cepheid variables are used to determine distances.
-
19M.3.SL.TZ2.14aii:
A line in the hydrogen spectrum when measured on Earth has a wavelength of 486 nm. Calculate, in nm, the wavelength of the same hydrogen line when observed in the galaxy’s emission spectrum.
- 19M.3.SL.TZ2.15b: Suggest the conditions that will cause the Sun to become a red giant.
-
19M.3.SL.TZ2.13bi:
Determine the peak apparent brightness of δ-Cephei as observed from Earth.
-
19M.3.SL.TZ2.13bii:
Calculate the peak surface temperature of δ-Cephei.
- 19M.3.SL.TZ2.13ai: Outline the processes that produce the change of luminosity with time of Cepheid variables.
- 19M.3.SL.TZ2.14b: Outline how observations of spectra from distant galaxies provide evidence that the universe is...
-
19M.3.SL.TZ2.15c:
Outline why the Sun will maintain a constant radius after it becomes a white dwarf.
- 19M.3.SL.TZ2.15a: Identify, on the HR diagram, the position of the Sun. Label the position S.
- 19M.3.HL.TZ1.19b: Suggest why type I a supernovae were used in the study that led to the conclusion that the...
-
19M.3.SL.TZ2.15d:
During its evolution, the Sun is likely to be a red giant of surface temperature 3000 K and luminosity 104 L☉. Later it is likely to be a white dwarf of surface temperature 10 000 K and luminosity 10-4 L☉. Calculate the .
-
17N.3.SL.TZ0.12c:
The mass of Sirius B is about the same mass as the Sun. The luminosity of Sirius B is 2.5 % of the luminosity of the Sun. Show, with a calculation, that Sirius B is not a main sequence star.
-
17N.3.SL.TZ0.12b:
The peak spectral line of Sirius B has a measured wavelength of 115 nm. Show that the surface temperature of Sirius B is about 25 000 K.
- 17N.3.SL.TZ0.12a: State what is meant by a binary star.
-
19N.3.SL.TZ0.10b(ii):
The surface temperature of Eta Cassiopeiae B is 4100 K. Determine the ratio .
-
19N.3.SL.TZ0.10c(iii):
Calculate the ratio .
-
19N.3.SL.TZ0.10b(i):
The peak wavelength of radiation from Eta Cassiopeiae A is 490 nm. Show that the surface temperature of Eta Cassiopeiae A is about 6000 K.
-
19N.3.SL.TZ0.11b(i):
Estimate the age of the universe in seconds using the Hubble constant H0 = 70 km s–1 Mpc–1.
- 19N.3.SL.TZ0.10 a: Distinguish between a constellation and a stellar cluster.
- 19N.3.SL.TZ0.10c(i): On the HR diagram, draw the present position of Eta Cassiopeiae A.
- 19N.3.SL.TZ0.10c(ii): State the star type of Eta Cassiopeiae A.
-
19N.3.SL.TZ0.10c(iv):
Deduce the final evolutionary state of Eta Cassiopeiae A.
-
19N.3.SL.TZ0.10b(iii):
The distance of the Eta Cassiopeiae system from the Earth is 1.8 × 1017 m. Calculate, in terms of , the luminosity of Eta Cassiopeiae A.
- 19N.3.SL.TZ0.11a(i): Outline how the light spectra of distant galaxies are used to confirm hypotheses about the...
-
19N.3.SL.TZ0.11b(ii):
Outline why the estimate made in (b)(i) is unlikely to be the actual age of the universe.
-
19N.3.SL.TZ0.11a(ii):
Light from a hydrogen source in a laboratory on Earth contains a spectral line of wavelength 122 nm. Light from the same spectral line reaching Earth from a distant galaxy has a wavelength of 392 nm. Determine the ratio of the present size of the universe to the size of the universe when the light was emitted by the galaxy.
- 19N.3.HL.TZ0.16a(i): Outline how the light spectra of distant galaxies are used to confirm hypotheses about the...
-
19N.3.HL.TZ0.16a(ii):
Light from a hydrogen source in a laboratory on Earth contains a spectral line of wavelength 122 nm. Light from the same spectral line reaching Earth from a distant galaxy has a wavelength of 392 nm. Determine the ratio of the present size of the universe to the size of the universe when the light was emitted by the galaxy.
- 19N.3.SL.TZ0.10a: Distinguish between a constellation and a stellar cluster.
Sub sections and their related questions
D.1 – Stellar quantities
- 16N.3.SL.TZ0.15a: State what is meant by a binary star system.
-
16N.3.SL.TZ0.15b:
(i) Calculate .
(ii) The luminosity of the Sun is 3.8 × 1026 W. Calculate the radius of Alpha Centauri A.
-
17M.3.SL.TZ1.9a.i:
State what is meant by a main sequence star.
-
17M.3.SL.TZ1.9a.iii:
The surface temperature of the Sun is about 6000 K. Estimate the surface temperature of Theta 1 Orionis.
-
17M.3.SL.TZ1.9a.iv:
Determine the distance of Theta 1 Orionis in AU.
-
17M.3.SL.TZ1.9b:
Discuss how Theta 1 Orionis does not collapse under its own weight.
-
17M.3.SL.TZ2.11a:
State the most abundant element in the core and the most abundant element in the outer layer.
-
17M.3.SL.TZ2.11c.iii:
The radius of a typical neutron star is 20 km and its surface temperature is 106 K. Determine the luminosity of this neutron star.
-
18M.3.SL.TZ1.10a.i:
Distinguish between the solar system and a galaxy.
-
18M.3.SL.TZ1.10a.ii:
Distinguish between a planet and a comet.
-
18M.3.SL.TZ2.11a:
Main sequence stars are in equilibrium under the action of forces. Outline how this equilibrium is achieved.
-
18M.3.SL.TZ2.11b:
A main sequence star P, is 1.3 times the mass of the Sun. Calculate the luminosity of P relative to the Sun.
-
18M.3.SL.TZ2.11c.i:
The luminosity of the Sun L is 3.85 × 1026 W. Determine the luminosity of Gacrux relative to the Sun.
-
18M.3.SL.TZ2.11c.ii:
The distance to Gacrux can be determined using stellar parallax. Outline why this method is not suitable for all stars.
- 18N.3.SL.TZ0.11a: Distinguish between a constellation and an open cluster.
- 18N.3.SL.TZ0.11b.i: The parallax angle of Mintaka measured from Earth is 3.64 × 10–3 arc-second. Calculate, in...
- 18N.3.SL.TZ0.11b.ii: State why there is a maximum distance that astronomers can measure using stellar parallax.
-
18N.3.SL.TZ0.12a.iii:
The following data are available for the Sun.
Surface temperature = 5800 K
Luminosity =
Mass =
Radius =
Epsilon Indi has a radius of 0.73 . Show that the luminosity of Epsilon Indi is 0.2 .
- 18N.3.HL.TZ0.17a: Distinguish between a constellation and an open cluster.
- 18N.3.HL.TZ0.17b.i: The parallax angle of Mintaka measured from Earth is 3.64 × 10–3 arc-second. Calculate, in...
- 18N.3.HL.TZ0.17b.ii: State why there is a maximum distance that astronomers can measure using stellar parallax.
-
18N.3.HL.TZ0.18a.iii:
The following data are available for the Sun.
Surface temperature = 5800 K
Luminosity =
Mass =
Radius =
Epsilon Indi has a radius of 0.73 . Show that the luminosity of Epsilon Indi is 0.2 .
-
19M.3.SL.TZ2.13bi:
Determine the peak apparent brightness of δ-Cephei as observed from Earth.
-
19M.3.SL.TZ2.15d:
During its evolution, the Sun is likely to be a red giant of surface temperature 3000 K and luminosity 104 L☉. Later it is likely to be a white dwarf of surface temperature 10 000 K and luminosity 10-4 L☉. Calculate the .
- 19N.3.SL.TZ0.10 a: Distinguish between a constellation and a stellar cluster.
-
19N.3.SL.TZ0.10b(ii):
The surface temperature of Eta Cassiopeiae B is 4100 K. Determine the ratio .
-
19N.3.SL.TZ0.10b(iii):
The distance of the Eta Cassiopeiae system from the Earth is 1.8 × 1017 m. Calculate, in terms of , the luminosity of Eta Cassiopeiae A.
- 19N.3.SL.TZ0.10a: Distinguish between a constellation and a stellar cluster.
-
20N.3.SL.TZ0.14a:
The astronomical unit () and light year () are convenient measures of distance in astrophysics. Define each unit.
:
:
- 20N.3.SL.TZ0.14b(i): Comets develop a tail as they approach the Sun. Identify one other characteristic of comets.
- 20N.3.SL.TZ0.14b(ii): Identify one object visible in the image that is outside our Solar System.
-
20N.3.SL.TZ0.15a:
Show that the apparent brightness , where is the distance of the object from Earth, is the surface temperature of the object and is the surface area of the object.
-
20N.3.SL.TZ0.15b:
Two of the brightest objects in the night sky seen from Earth are the planet Venus and the star Sirius. Explain why the equation is applicable to Sirius but not to Venus.
-
20N.3.SL.TZ0.17b(i):
Estimate, in , the distance to Eta Aquilae A using the parallax angle in the table.
-
20N.3.SL.TZ0.17b(ii):
Estimate, in , the distance to Eta Aquilae A using the luminosity in the table, given that .
-
20N.3.HL.TZ0.22b(i):
Estimate, in , the distance to Eta Aquilae A using the parallax angle in the table.
-
20N.3.HL.TZ0.22b(ii):
Estimate, in , the distance to Eta Aquilae A using the luminosity in the table, given that .
- 21N.1.SL.TZ0.30: Which is correct for a black-body radiator? A. The power it emits from a unit surface area...
D.2 – Stellar characteristics and stellar evolution
-
16N.3.SL.TZ0.15c:
Show, without calculation, that the radius of Alpha Centauri B is smaller than the radius of Alpha Centauri A.
- 16N.3.SL.TZ0.15d: Alpha Centauri A is in equilibrium at constant radius. Explain how this equilibrium is maintained.
-
16N.3.SL.TZ0.15e:
A standard Hertzsprung–Russell (HR) diagram is shown.
Using the HR diagram, draw the present position of Alpha Centauri A and its expected evolutionary path.
-
16N.3.SL.TZ0.16a:
Determine the distance from Earth to the Cepheid star in parsecs. The luminosity of the Sun is 3.8 × 1026 W. The average apparent brightness of the Cepheid star is 1.1 × 10–9 W m–2.
- 16N.3.SL.TZ0.16b: Explain why Cephids are used as standard candles.
-
17M.3.SL.TZ1.9a.ii:
Show that the mass of Theta 1 Orionis is about 40 solar masses.
-
17M.3.SL.TZ1.9c:
The Sun and Theta 1 Orionis will eventually leave the main sequence. Compare and contrast the different stages in the evolution of the two stars.
-
17M.3.SL.TZ1.10a.ii:
The present temperature of the CMB is 2.8 K. Calculate the peak wavelength of the CMB.
-
17M.3.SL.TZ2.11b:
The Hertzsprung–Russell (HR) diagram shows two main sequence stars X and Y and includes lines of constant radius. R is the radius of the Sun.

Using the mass–luminosity relation and information from the graph, determine the ratio .
-
17M.3.SL.TZ2.11c.i:
On the HR diagram in (b), draw a line to indicate the evolutionary path of star X.
-
17M.3.SL.TZ2.11c.ii:
Outline why the neutron star that is left after the supernova stage does not collapse under the action of gravitation.
-
17M.3.SL.TZ2.11c.iv:
Determine the region of the electromagnetic spectrum in which the neutron star in (c)(iii) emits most of its energy.
-
17M.3.SL.TZ2.12c.ii:
Describe how type Ia supernovae could be used to measure the distance to this galaxy.
- 17N.3.SL.TZ0.12a: State what is meant by a binary star.
-
17N.3.SL.TZ0.12b:
The peak spectral line of Sirius B has a measured wavelength of 115 nm. Show that the surface temperature of Sirius B is about 25 000 K.
-
17N.3.SL.TZ0.12c:
The mass of Sirius B is about the same mass as the Sun. The luminosity of Sirius B is 2.5 % of the luminosity of the Sun. Show, with a calculation, that Sirius B is not a main sequence star.
-
17N.3.SL.TZ0.12d.i:
Determine the radius of Sirius B in terms of the radius of the Sun.
- 17N.3.SL.TZ0.12d.ii: Identify the star type of Sirius B.
- 17N.3.SL.TZ0.12e.i: draw the approximate positions of Sirius A, labelled A and Sirius B, labelled B.
- 17N.3.SL.TZ0.12e.ii: sketch the expected evolutionary path for Sirius A.
-
18M.3.SL.TZ1.11a.i:
Suggest, using the graphs, why star X is most likely to be a main sequence star.
-
18M.3.SL.TZ1.11a.ii:
Show that the temperature of star X is approximately 10 000 K.
-
18M.3.SL.TZ1.11b.i:
Write down the luminosity of star X (LX) in terms of the luminosity of the Sun (Ls).
-
18M.3.SL.TZ1.11b.ii:
Determine the radius of star X (RX) in terms of the radius of the Sun (Rs).
-
18M.3.SL.TZ1.11b.iii:
Estimate the mass of star X (MX) in terms of the mass of the Sun (Ms).
-
18M.3.SL.TZ1.11c:
Star X is likely to evolve into a stable white dwarf star.
Outline why the radius of a white dwarf star reaches a stable value.
-
18M.3.SL.TZ2.11d.i:
draw the main sequence.
-
18M.3.SL.TZ2.11d.ii:
plot the position, using the letter P, of the main sequence star P you calculated in (b).
-
18M.3.SL.TZ2.11d.iii:
plot the position, using the letter G, of Gacrux.
-
18M.3.SL.TZ2.11e:
Discuss, with reference to its change in mass, the evolution of star P from the main sequence until its final stable phase.
-
18N.3.SL.TZ0.12a.i:
Determine the peak wavelength of the radiation emitted by Epsilon Indi.
- 18N.3.SL.TZ0.12a.ii: Using the axis, draw the variation with wavelength of the intensity of the radiation emitted by...
-
18N.3.SL.TZ0.12b:
Epsilon Indi is a main sequence star. Show that the mass of Epsilon Indi is 0.64 .
- 18N.3.SL.TZ0.12c: Describe how the chemical composition of a star may be determined.
- 18N.3.SL.TZ0.12d: Describe the stages in the evolution of Epsilon Indi from the point when it leaves the main...
-
18N.3.HL.TZ0.18a.i:
Determine the peak wavelength of the radiation emitted by Epsilon Indi.
- 18N.3.HL.TZ0.18a.ii: Using the axis, draw the variation with wavelength of the intensity of the radiation emitted by...
-
18N.3.HL.TZ0.18b:
Epsilon Indi is a main sequence star. Show that the mass of Epsilon Indi is 0.64 .
-
18N.3.HL.TZ0.18c:
The Sun will spend about nine billion years on the main sequence. Calculate how long Epsilon Indi will spend on the main sequence.
- 18N.3.HL.TZ0.18d: Describe the stages in the evolution of Epsilon Indi from the point when it leaves the main...
- 19M.3.SL.TZ2.13ai: Outline the processes that produce the change of luminosity with time of Cepheid variables.
- 19M.3.SL.TZ2.13aii: Explain how Cepheid variables are used to determine distances.
-
19M.3.SL.TZ2.13bii:
Calculate the peak surface temperature of δ-Cephei.
- 19M.3.SL.TZ2.15a: Identify, on the HR diagram, the position of the Sun. Label the position S.
- 19M.3.SL.TZ2.15b: Suggest the conditions that will cause the Sun to become a red giant.
-
19M.3.SL.TZ2.15c:
Outline why the Sun will maintain a constant radius after it becomes a white dwarf.
-
19N.3.SL.TZ0.10b(i):
The peak wavelength of radiation from Eta Cassiopeiae A is 490 nm. Show that the surface temperature of Eta Cassiopeiae A is about 6000 K.
- 19N.3.SL.TZ0.10c(i): On the HR diagram, draw the present position of Eta Cassiopeiae A.
- 19N.3.SL.TZ0.10c(ii): State the star type of Eta Cassiopeiae A.
-
19N.3.SL.TZ0.10c(iii):
Calculate the ratio .
-
19N.3.SL.TZ0.10c(iv):
Deduce the final evolutionary state of Eta Cassiopeiae A.
-
20N.3.SL.TZ0.17a:
Show by calculation that Eta Aquilae A is not on the main sequence.
- 20N.3.SL.TZ0.17d: Eta Aquilae A is a Cepheid variable. Explain why the brightness of Eta Aquilae A varies.
-
20N.3.HL.TZ0.22a:
Show by calculation that Eta Aquilae A is not on the main sequence.
- 20N.3.HL.TZ0.22d: Eta Aquilae A is a Cepheid variable. Explain why the brightness of Eta Aquilae A varies.
- 21N.1.SL.TZ0.30: Which is correct for a black-body radiator? A. The power it emits from a unit surface area...
D.3 – Cosmology
- 16N.3.SL.TZ0.17a: Identify two other characteristics of the CMB radiation that are predicted from the Hot Big Bang...
- 16N.3.SL.TZ0.17b: A spectral line in the hydrogen spectrum measured in the laboratory today has a wavelength of...
-
17M.3.SL.TZ1.10a.i:
State two characteristics of the cosmic microwave background (CMB) radiation.
-
17M.3.SL.TZ1.10b:
Describe how the CMB provides evidence for the Hot Big Bang model of the universe.
-
17M.3.SL.TZ1.10c.i:
Determine the distance to this galaxy using a value for the Hubble constant of H0 = 68 km s–1Mpc–1.
-
17M.3.SL.TZ1.10c.ii:
Estimate the size of the Universe relative to its present size when the light was emitted by the galaxy in (c).
-
17M.3.SL.TZ2.12a:
Describe what is meant by the Big Bang model of the universe.
-
17M.3.SL.TZ2.12b:
State two features of the cosmic microwave background (CMB) radiation which are consistent with the Big Bang model.
-
17M.3.SL.TZ2.12c.i:
Determine the distance to the galaxy in Mpc.
- 17N.3.SL.TZ0.13a: Outline one reason for the difference in wavelength.
-
17N.3.SL.TZ0.13b:
Determine the velocity of the galaxy relative to Earth.
-
18M.3.SL.TZ1.12a:
Explain how international collaboration has helped to refine this value.
-
18M.3.SL.TZ1.12b:
Estimate, in Mpc, the distance between the galaxy and the Earth.
-
18M.3.SL.TZ2.12a:
Estimate, using the data, the age of the universe. Give your answer in seconds.
-
18M.3.SL.TZ2.12b:
Identify the assumption that you made in your answer to (a).
-
18M.3.SL.TZ2.12c:
On the graph, one galaxy is labelled A. Determine the size of the universe, relative to its present size, when light from the galaxy labelled A was emitted.
-
18N.3.SL.TZ0.13a:
Outline how Hubble measured the recessional velocities of galaxies.
-
18N.3.SL.TZ0.13b:
Using the graph, determine in s, the age of the universe.
-
18N.3.HL.TZ0.19a:
Outline how Hubble measured the recessional velocities of galaxies.
-
18N.3.HL.TZ0.19b:
Use the graph to determine the age of the universe in s.
- 19M.3.SL.TZ2.14ai: A galaxy is 1.6 × 108 ly from Earth. Show that its recessional speed as measured from Earth is...
-
19M.3.SL.TZ2.14aii:
A line in the hydrogen spectrum when measured on Earth has a wavelength of 486 nm. Calculate, in nm, the wavelength of the same hydrogen line when observed in the galaxy’s emission spectrum.
- 19M.3.SL.TZ2.14b: Outline how observations of spectra from distant galaxies provide evidence that the universe is...
- 19M.3.HL.TZ1.19b: Suggest why type I a supernovae were used in the study that led to the conclusion that the...
- 19N.3.SL.TZ0.11a(i): Outline how the light spectra of distant galaxies are used to confirm hypotheses about the...
-
19N.3.SL.TZ0.11a(ii):
Light from a hydrogen source in a laboratory on Earth contains a spectral line of wavelength 122 nm. Light from the same spectral line reaching Earth from a distant galaxy has a wavelength of 392 nm. Determine the ratio of the present size of the universe to the size of the universe when the light was emitted by the galaxy.
-
19N.3.SL.TZ0.11b(i):
Estimate the age of the universe in seconds using the Hubble constant H0 = 70 km s–1 Mpc–1.
-
19N.3.SL.TZ0.11b(ii):
Outline why the estimate made in (b)(i) is unlikely to be the actual age of the universe.
- 19N.3.HL.TZ0.16a(i): Outline how the light spectra of distant galaxies are used to confirm hypotheses about the...
-
19N.3.HL.TZ0.16a(ii):
Light from a hydrogen source in a laboratory on Earth contains a spectral line of wavelength 122 nm. Light from the same spectral line reaching Earth from a distant galaxy has a wavelength of 392 nm. Determine the ratio of the present size of the universe to the size of the universe when the light was emitted by the galaxy.
-
20N.3.SL.TZ0.16a:
The light from a distant galaxy shows that .
Calculate the ratio .
-
20N.3.SL.TZ0.16b:
Outline how Hubble’s law is related to .
-
20N.3.HL.TZ0.21a:
The light from a distant galaxy shows that .
Calculate the ratio .
-
20N.3.HL.TZ0.21b:
Outline how Hubble’s law is related to .
- 21N.1.SL.TZ0.30: Which is correct for a black-body radiator? A. The power it emits from a unit surface area...
