DP Physics Questionbank

Option D: Astrophysics
| Path: |
Description
[N/A]Directly related questions
- 16N.3.HL.TZ0.24a: Describe how some white dwarf stars become type Ia supernovae.
-
16N.3.SL.TZ0.15e:
A standard Hertzsprung–Russell (HR) diagram is shown.
Using the HR diagram, draw the present position of Alpha Centauri A and its expected evolutionary path.
- 16N.3.HL.TZ0.24b: Hence, explain why a type Ia supernova is used as a standard candle.
-
16N.3.HL.TZ0.25a:
Calculate the rotation velocity of stars 4.0 kpc from the centre of the galaxy. The average density of the galaxy is 5.0 × 10–21 kg m–3.
-
16N.3.SL.TZ0.15b:
(i) Calculate .
(ii) The luminosity of the Sun is 3.8 × 1026 W. Calculate the radius of Alpha Centauri A.
-
16N.3.SL.TZ0.16a:
Determine the distance from Earth to the Cepheid star in parsecs. The luminosity of the Sun is 3.8 × 1026 W. The average apparent brightness of the Cepheid star is 1.1 × 10–9 W m–2.
- 16N.3.SL.TZ0.17b: A spectral line in the hydrogen spectrum measured in the laboratory today has a wavelength of...
- 16N.3.HL.TZ0.25b: Explain why the rotation curves are evidence for the existence of dark matter.
- 16N.3.SL.TZ0.15a: State what is meant by a binary star system.
- 16N.3.SL.TZ0.15d: Alpha Centauri A is in equilibrium at constant radius. Explain how this equilibrium is maintained.
-
16N.3.SL.TZ0.15c:
Show, without calculation, that the radius of Alpha Centauri B is smaller than the radius of Alpha Centauri A.
- 16N.3.SL.TZ0.17a: Identify two other characteristics of the CMB radiation that are predicted from the Hot Big Bang...
- 16N.3.HL.TZ0.24c: Explain how the observation of type Ia supernovae led to the hypothesis that dark energy exists.
- 16N.3.SL.TZ0.16b: Explain why Cephids are used as standard candles.
-
17M.3.SL.TZ1.9a.iv:
Determine the distance of Theta 1 Orionis in AU.
-
17M.3.SL.TZ1.10c.ii:
Estimate the size of the Universe relative to its present size when the light was emitted by the galaxy in (c).
-
17M.3.SL.TZ1.9a.i:
State what is meant by a main sequence star.
-
17M.3.SL.TZ1.10a.i:
State two characteristics of the cosmic microwave background (CMB) radiation.
-
17M.3.SL.TZ1.10c.i:
Determine the distance to this galaxy using a value for the Hubble constant of H0 = 68 km s–1Mpc–1.
-
17M.3.SL.TZ1.10a.ii:
The present temperature of the CMB is 2.8 K. Calculate the peak wavelength of the CMB.
-
17M.3.SL.TZ1.9a.ii:
Show that the mass of Theta 1 Orionis is about 40 solar masses.
-
17M.3.SL.TZ1.9b:
Discuss how Theta 1 Orionis does not collapse under its own weight.
-
17M.3.SL.TZ1.10b:
Describe how the CMB provides evidence for the Hot Big Bang model of the universe.
-
17M.3.SL.TZ1.9a.iii:
The surface temperature of the Sun is about 6000 K. Estimate the surface temperature of Theta 1 Orionis.
-
17M.3.SL.TZ1.9c:
The Sun and Theta 1 Orionis will eventually leave the main sequence. Compare and contrast the different stages in the evolution of the two stars.
-
17M.3.SL.TZ2.11b:
The Hertzsprung–Russell (HR) diagram shows two main sequence stars X and Y and includes lines of constant radius. R is the radius of the Sun.
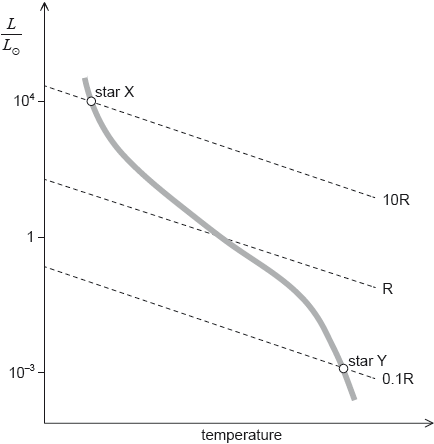
Using the mass–luminosity relation and information from the graph, determine the ratio .
-
17M.3.SL.TZ2.11c.iii:
The radius of a typical neutron star is 20 km and its surface temperature is 106 K. Determine the luminosity of this neutron star.
-
17M.3.SL.TZ2.11a:
State the most abundant element in the core and the most abundant element in the outer layer.
-
17M.3.SL.TZ2.11c.iv:
Determine the region of the electromagnetic spectrum in which the neutron star in (c)(iii) emits most of its energy.
-
17M.3.SL.TZ2.12b:
State two features of the cosmic microwave background (CMB) radiation which are consistent with the Big Bang model.
-
17M.3.SL.TZ2.12a:
Describe what is meant by the Big Bang model of the universe.
-
17M.3.SL.TZ2.11c.ii:
Outline why the neutron star that is left after the supernova stage does not collapse under the action of gravitation.
-
17M.3.SL.TZ2.11c.i:
On the HR diagram in (b), draw a line to indicate the evolutionary path of star X.
-
17M.3.SL.TZ2.12c.ii:
Describe how type Ia supernovae could be used to measure the distance to this galaxy.
-
17M.3.SL.TZ2.12c.i:
Determine the distance to the galaxy in Mpc.
-
17M.3.HL.TZ1.17a:
The graph shows the variation with time t of the cosmic scale factor R in the flat model of the universe in which dark energy is ignored.
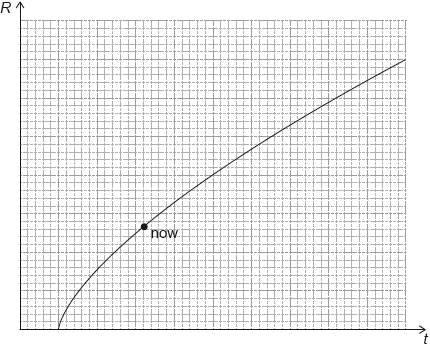
On the axes above draw a graph to show the variation of R with time, when dark energy is present.
-
17M.3.HL.TZ1.17b.ii:
The density of dark energy is ρΛc2 where ρΛ = ρc – ρm. Calculate the amount of dark energy in 1 m3 of space.
-
17M.3.HL.TZ2.20a:
Describe what is meant by dark matter.
-
17M.3.HL.TZ1.16a:
Outline, with reference to star formation, what is meant by the Jeans criterion.
-
17M.3.HL.TZ1.16b:
In the proton–proton cycle, four hydrogen nuclei fuse to produce one nucleus of helium releasing a total of 4.3 × 10–12 J of energy. The Sun will spend 1010 years on the main sequence. It may be assumed that during this time the Sun maintains a constant luminosity of 3.8 × 1026 W.
Show that the total mass of hydrogen that is converted into helium while the Sun is on the main sequence is 2 × 1029 kg. -
17M.3.HL.TZ1.16c:
Massive stars that have left the main sequence have a layered structure with different chemical elements in different layers. Discuss this structure by reference to the nuclear reactions taking place in such stars.
-
17M.3.HL.TZ2.19a.ii:
The present temperature of the CMB is 2.8 K. This radiation was emitted when the universe was smaller by a factor of 1100. Estimate the temperature of the CMB at the time of its emission.
-
17M.3.HL.TZ2.19b:
State how the anisotropies in the CMB distribution are interpreted.
-
17M.3.HL.TZ2.20c:
Curve A shows the actual rotation curve of a nearby galaxy. Curve B shows the predicted rotation curve based on the visible stars in the galaxy.
Explain how curve A provides evidence for dark matter.
-
17M.3.HL.TZ1.17b.i:
The density of the observable matter in the universe is only 0.05 ρc. Suggest how the remaining 0.27 ρc is accounted for.
-
17M.3.HL.TZ2.19a.i:
Derive, using the concept of the cosmological origin of redshift, the relation
T
between the temperature T of the cosmic microwave background (CMB) radiation and the cosmic scale factor R.
-
17M.3.HL.TZ2.20b:
The distribution of mass in a spherical system is such that the density ρ varies with distance r from the centre as
ρ =
where k is a constant.
Show that the rotation curve of this system is described by
v = constant.
-
20N.3.SL.TZ0.17a:
Show by calculation that Eta Aquilae A is not on the main sequence.
- 20N.3.SL.TZ0.17d: Eta Aquilae A is a Cepheid variable. Explain why the brightness of Eta Aquilae A varies.
-
20N.3.SL.TZ0.16b:
Outline how Hubble’s law is related to .
- 20N.3.SL.TZ0.14b(i): Comets develop a tail as they approach the Sun. Identify one other characteristic of comets.
-
20N.3.SL.TZ0.15a:
Show that the apparent brightness , where is the distance of the object from Earth, is the surface temperature of the object and is the surface area of the object.
-
20N.3.SL.TZ0.16a:
The light from a distant galaxy shows that .
Calculate the ratio .
-
20N.3.SL.TZ0.14a:
The astronomical unit () and light year () are convenient measures of distance in astrophysics. Define each unit.
:
:
-
20N.3.SL.TZ0.15b:
Two of the brightest objects in the night sky seen from Earth are the planet Venus and the star Sirius. Explain why the equation is applicable to Sirius but not to Venus.
-
20N.3.SL.TZ0.17b(i):
Estimate, in , the distance to Eta Aquilae A using the parallax angle in the table.
-
20N.3.HL.TZ0.21b:
Outline how Hubble’s law is related to .
- 20N.3.SL.TZ0.14b(ii): Identify one object visible in the image that is outside our Solar System.
- 20N.3.HL.TZ0.22d: Eta Aquilae A is a Cepheid variable. Explain why the brightness of Eta Aquilae A varies.
-
20N.3.SL.TZ0.17b(ii):
Estimate, in , the distance to Eta Aquilae A using the luminosity in the table, given that .
-
20N.3.HL.TZ0.22b(ii):
Estimate, in , the distance to Eta Aquilae A using the luminosity in the table, given that .
-
20N.3.HL.TZ0.22b(i):
Estimate, in , the distance to Eta Aquilae A using the parallax angle in the table.
- 20N.3.HL.TZ0.22e: Eta Aquilae A was on the main sequence before it became a variable star. Compare, without...
-
20N.3.HL.TZ0.24b:
Identify two possible causes of the anisotropies in (a).
- 20N.3.HL.TZ0.23: In 2017, two neutron stars were observed to merge, forming a black hole. The material released...
-
20N.3.HL.TZ0.21a:
The light from a distant galaxy shows that .
Calculate the ratio .
- 20N.3.HL.TZ0.21c: Hubble originally linked galactic redshift to a Doppler effect arising from galactic recession....
-
20N.3.HL.TZ0.22a:
Show by calculation that Eta Aquilae A is not on the main sequence.
- 20N.3.HL.TZ0.24a: State the nature of the anisotropies observed in the CMB radiation.
-
17N.3.HL.TZ0.20a:
The Sun is a second generation star. Outline, with reference to the Jeans criterion (MJ), how the Sun is likely to have been formed.
-
17N.3.HL.TZ0.20c:
Show that the critical density of the universe is
where H is the Hubble parameter and G is the gravitational constant.
-
17N.3.HL.TZ0.20b:
Suggest how fluctuations in the cosmic microwave background (CMB) radiation are linked to the observation that galaxies collide.
-
17N.3.SL.TZ0.13b:
Determine the velocity of the galaxy relative to Earth.
-
17N.3.SL.TZ0.12d.i:
Determine the radius of Sirius B in terms of the radius of the Sun.
- 17N.3.SL.TZ0.12d.ii: Identify the star type of Sirius B.
- 17N.3.SL.TZ0.12e.i: draw the approximate positions of Sirius A, labelled A and Sirius B, labelled B.
- 17N.3.SL.TZ0.12e.ii: sketch the expected evolutionary path for Sirius A.
- 17N.3.SL.TZ0.13a: Outline one reason for the difference in wavelength.
-
18M.3.HL.TZ1.19a:
The mass of visible matter in the galaxy is M.
Show that for stars where r > R0 the velocity of orbit is v = .
-
18M.3.HL.TZ1.18a:
Describe the formation of a type Ia supernova.
-
18M.3.HL.TZ1.19c:
Explain, using the equation in (a) and the graphs, why the presence of visible matter alone cannot account for the velocity of stars when r > R0.
-
18M.3.HL.TZ1.18b.i:
Show that the distance to the supernova is approximately 3.1 × 1018 m.
-
18M.3.HL.TZ1.19b:
Draw on the axes the observed variation with r of the orbital speed v of stars in a galaxy.
-
18M.3.HL.TZ1.18b.ii:
State one assumption made in your calculation.
-
18M.3.HL.TZ2.18a:
Outline, with reference to the Jeans criterion, why a cold dense gas cloud is more likely to form new stars than a hot diffuse gas cloud.
-
18M.3.HL.TZ2.18b:
Explain how neutron capture can produce elements with an atomic number greater than iron.
-
18M.3.HL.TZ2.19a:
Explain the evidence that indicates the location of dark matter in galaxies.
-
18M.3.HL.TZ2.19b:
Outline why a hypothesis of dark energy has been developed.
-
18M.3.SL.TZ2.11d.ii:
plot the position, using the letter P, of the main sequence star P you calculated in (b).
-
18M.3.SL.TZ2.11d.iii:
plot the position, using the letter G, of Gacrux.
-
18M.3.SL.TZ2.11c.i:
The luminosity of the Sun L is 3.85 × 1026 W. Determine the luminosity of Gacrux relative to the Sun.
-
18M.3.SL.TZ2.11c.ii:
The distance to Gacrux can be determined using stellar parallax. Outline why this method is not suitable for all stars.
-
18M.3.SL.TZ2.12a:
Estimate, using the data, the age of the universe. Give your answer in seconds.
-
18M.3.SL.TZ2.11a:
Main sequence stars are in equilibrium under the action of forces. Outline how this equilibrium is achieved.
-
18M.3.SL.TZ2.11e:
Discuss, with reference to its change in mass, the evolution of star P from the main sequence until its final stable phase.
-
18M.3.SL.TZ2.11b:
A main sequence star P, is 1.3 times the mass of the Sun. Calculate the luminosity of P relative to the Sun.
-
18M.3.SL.TZ2.11d.i:
draw the main sequence.
-
18M.3.SL.TZ2.12b:
Identify the assumption that you made in your answer to (a).
-
18M.3.SL.TZ2.12c:
On the graph, one galaxy is labelled A. Determine the size of the universe, relative to its present size, when light from the galaxy labelled A was emitted.
-
18M.3.SL.TZ1.10a.i:
Distinguish between the solar system and a galaxy.
-
18M.3.SL.TZ1.10a.ii:
Distinguish between a planet and a comet.
-
18M.3.SL.TZ1.11a.i:
Suggest, using the graphs, why star X is most likely to be a main sequence star.
-
18M.3.SL.TZ1.11a.ii:
Show that the temperature of star X is approximately 10 000 K.
-
18M.3.SL.TZ1.11b.i:
Write down the luminosity of star X (LX) in terms of the luminosity of the Sun (Ls).
-
18M.3.SL.TZ1.11b.ii:
Determine the radius of star X (RX) in terms of the radius of the Sun (Rs).
-
18M.3.SL.TZ1.11b.iii:
Estimate the mass of star X (MX) in terms of the mass of the Sun (Ms).
-
18M.3.SL.TZ1.11c:
Star X is likely to evolve into a stable white dwarf star.
Outline why the radius of a white dwarf star reaches a stable value.
-
18M.3.SL.TZ1.12a:
Explain how international collaboration has helped to refine this value.
-
18M.3.SL.TZ1.12b:
Estimate, in Mpc, the distance between the galaxy and the Earth.
- 21N.1.SL.TZ0.30: Which is correct for a black-body radiator? A. The power it emits from a unit surface area...
- 18N.3.SL.TZ0.12d: Describe the stages in the evolution of Epsilon Indi from the point when it leaves the main...
-
18N.3.SL.TZ0.12b:
Epsilon Indi is a main sequence star. Show that the mass of Epsilon Indi is 0.64 .
- 18N.3.SL.TZ0.12a.ii: Using the axis, draw the variation with wavelength of the intensity of the radiation emitted by...
-
18N.3.HL.TZ0.18a.i:
Determine the peak wavelength of the radiation emitted by Epsilon Indi.
- 18N.3.SL.TZ0.12c: Describe how the chemical composition of a star may be determined.
-
18N.3.HL.TZ0.19b:
Use the graph to determine the age of the universe in s.
- 18N.3.SL.TZ0.11a: Distinguish between a constellation and an open cluster.
-
18N.3.SL.TZ0.13a:
Outline how Hubble measured the recessional velocities of galaxies.
- 18N.3.SL.TZ0.11b.ii: State why there is a maximum distance that astronomers can measure using stellar parallax.
-
18N.3.SL.TZ0.12a.iii:
The following data are available for the Sun.
Surface temperature = 5800 K
Luminosity =
Mass =
Radius =
Epsilon Indi has a radius of 0.73 . Show that the luminosity of Epsilon Indi is 0.2 .
- 18N.3.SL.TZ0.11b.i: The parallax angle of Mintaka measured from Earth is 3.64 × 10–3 arc-second. Calculate, in...
-
18N.3.SL.TZ0.12a.i:
Determine the peak wavelength of the radiation emitted by Epsilon Indi.
-
18N.3.HL.TZ0.21b:
The present temperature of the cosmic microwave background (CMB) radiation is 3 K. Estimate the size of the universe relative to the present size of the universe when the temperature of the CMB was 300 K.
-
18N.3.SL.TZ0.13b:
Using the graph, determine in s, the age of the universe.
- 18N.3.HL.TZ0.17c: The Great Nebula is located in Orion. Describe, using the Jeans criterion, the...
- 18N.3.HL.TZ0.20a: Outline what is meant by dark energy.
- 18N.3.HL.TZ0.17b.ii: State why there is a maximum distance that astronomers can measure using stellar parallax.
- 18N.3.HL.TZ0.17b.i: The parallax angle of Mintaka measured from Earth is 3.64 × 10–3 arc-second. Calculate, in...
-
18N.3.HL.TZ0.19a:
Outline how Hubble measured the recessional velocities of galaxies.
- 18N.3.HL.TZ0.17a: Distinguish between a constellation and an open cluster.
-
18N.3.HL.TZ0.18b:
Epsilon Indi is a main sequence star. Show that the mass of Epsilon Indi is 0.64 .
- 18N.3.HL.TZ0.20b: State two candidates for dark matter.
-
18N.3.HL.TZ0.18a.iii:
The following data are available for the Sun.
Surface temperature = 5800 K
Luminosity =
Mass =
Radius =
Epsilon Indi has a radius of 0.73 . Show that the luminosity of Epsilon Indi is 0.2 .
- 18N.3.HL.TZ0.18a.ii: Using the axis, draw the variation with wavelength of the intensity of the radiation emitted by...
- 18N.3.HL.TZ0.18d: Describe the stages in the evolution of Epsilon Indi from the point when it leaves the main...
-
18N.3.HL.TZ0.21a:
Show that the temperature of the universe is inversely proportional to the cosmic scale factor.
-
18N.3.HL.TZ0.18c:
The Sun will spend about nine billion years on the main sequence. Calculate how long Epsilon Indi will spend on the main sequence.
- 19M.3.SL.TZ2.14ai: A galaxy is 1.6 × 108 ly from Earth. Show that its recessional speed as measured from Earth is...
- 19M.3.SL.TZ2.13aii: Explain how Cepheid variables are used to determine distances.
- 19M.3.SL.TZ2.15a: Identify, on the HR diagram, the position of the Sun. Label the position S.
-
19M.3.SL.TZ2.14aii:
A line in the hydrogen spectrum when measured on Earth has a wavelength of 486 nm. Calculate, in nm, the wavelength of the same hydrogen line when observed in the galaxy’s emission spectrum.
- 19M.3.SL.TZ2.15b: Suggest the conditions that will cause the Sun to become a red giant.
-
19M.3.SL.TZ2.13bi:
Determine the peak apparent brightness of δ-Cephei as observed from Earth.
-
19M.3.SL.TZ2.13bii:
Calculate the peak surface temperature of δ-Cephei.
- 19M.3.SL.TZ2.13ai: Outline the processes that produce the change of luminosity with time of Cepheid variables.
- 19M.3.SL.TZ2.14b: Outline how observations of spectra from distant galaxies provide evidence that the universe is...
-
19M.3.SL.TZ2.15c:
Outline why the Sun will maintain a constant radius after it becomes a white dwarf.
- 19M.3.HL.TZ2.21b: Describe the r process which occurs during type II supernovae nucleosynthesis.
- 19M.3.HL.TZ1.19b: Suggest why type I a supernovae were used in the study that led to the conclusion that the...
- 19M.3.HL.TZ1.19a.i: Describe the mechanism of formation of type I a supernovae.
- 19M.3.HL.TZ1.20a: Light from distant galaxies is redshifted. Explain the cosmological origin of this redshift.
-
19M.3.HL.TZ1.20b.ii:
Compare and contrast, the variation with time of the temperature of the cosmic background (CMB) radiation, for the two models from the present time onward.
- 19M.3.HL.TZ1.20b.i: Draw, on the axes, a graph to show the variation with time of the cosmic scale factor R for the...
-
19M.3.HL.TZ1.19a.ii:
Describe the mechanism of formation of type II supernovae.
-
19M.3.SL.TZ2.15d:
During its evolution, the Sun is likely to be a red giant of surface temperature 3000 K and luminosity 104 L☉. Later it is likely to be a white dwarf of surface temperature 10 000 K and luminosity 10-4 L☉. Calculate the .
- 19M.3.HL.TZ2.21a: Explain the formation of a type I a supernova which enables the star to be used as a standard...
-
19M.3.HL.TZ2.22b:
At critical density there is zero total energy. Show that the critical density of the universe is: .
-
19M.3.HL.TZ2.22a:
Justify that the total energy of this particle is .
- 19M.3.HL.TZ2.22c: The accepted value for the Hubble constant is 2.3 × 10−18 s−1. Estimate the critical density of...
-
17N.3.SL.TZ0.12c:
The mass of Sirius B is about the same mass as the Sun. The luminosity of Sirius B is 2.5 % of the luminosity of the Sun. Show, with a calculation, that Sirius B is not a main sequence star.
-
17N.3.SL.TZ0.12b:
The peak spectral line of Sirius B has a measured wavelength of 115 nm. Show that the surface temperature of Sirius B is about 25 000 K.
- 17N.3.SL.TZ0.12a: State what is meant by a binary star.
-
19N.3.SL.TZ0.10b(ii):
The surface temperature of Eta Cassiopeiae B is 4100 K. Determine the ratio .
-
19N.3.SL.TZ0.10c(iii):
Calculate the ratio .
-
19N.3.SL.TZ0.10b(i):
The peak wavelength of radiation from Eta Cassiopeiae A is 490 nm. Show that the surface temperature of Eta Cassiopeiae A is about 6000 K.
-
19N.3.SL.TZ0.11b(i):
Estimate the age of the universe in seconds using the Hubble constant H0 = 70 km s–1 Mpc–1.
- 19N.3.SL.TZ0.10 a: Distinguish between a constellation and a stellar cluster.
- 19N.3.SL.TZ0.10c(i): On the HR diagram, draw the present position of Eta Cassiopeiae A.
- 19N.3.SL.TZ0.10c(ii): State the star type of Eta Cassiopeiae A.
-
19N.3.SL.TZ0.10c(iv):
Deduce the final evolutionary state of Eta Cassiopeiae A.
-
19N.3.SL.TZ0.10b(iii):
The distance of the Eta Cassiopeiae system from the Earth is 1.8 × 1017 m. Calculate, in terms of , the luminosity of Eta Cassiopeiae A.
- 19N.3.SL.TZ0.11a(i): Outline how the light spectra of distant galaxies are used to confirm hypotheses about the...
-
19N.3.SL.TZ0.11b(ii):
Outline why the estimate made in (b)(i) is unlikely to be the actual age of the universe.
-
19N.3.SL.TZ0.11a(ii):
Light from a hydrogen source in a laboratory on Earth contains a spectral line of wavelength 122 nm. Light from the same spectral line reaching Earth from a distant galaxy has a wavelength of 392 nm. Determine the ratio of the present size of the universe to the size of the universe when the light was emitted by the galaxy.
- 19N.3.HL.TZ0.16a(i): Outline how the light spectra of distant galaxies are used to confirm hypotheses about the...
-
19N.3.HL.TZ0.17a:
Proxima Centauri is a main sequence star with a mass of 0.12 solar masses.
Estimate .
- 19N.3.HL.TZ0.17b: Describe why iron is the heaviest element that can be produced by nuclear fusion processes inside...
- 19N.3.HL.TZ0.16b(iii): It is estimated that less than 20 % of the matter in the universe is observable. Discuss how...
- 19N.3.HL.TZ0.16b(i): State what is meant by the critical density.
-
19N.3.HL.TZ0.16a(ii):
Light from a hydrogen source in a laboratory on Earth contains a spectral line of wavelength 122 nm. Light from the same spectral line reaching Earth from a distant galaxy has a wavelength of 392 nm. Determine the ratio of the present size of the universe to the size of the universe when the light was emitted by the galaxy.
-
19N.3.HL.TZ0.16b(ii):
Calculate the density of matter in the universe, using the Hubble constant 70 km s–1 Mpc–1.
-
19N.3.HL.TZ0.17c:
Discuss one process by which elements heavier than iron are formed in stars.
- 19N.3.SL.TZ0.10a: Distinguish between a constellation and a stellar cluster.
Sub sections and their related questions
Option D: Astrophysics (Core topics)
- 16N.3.SL.TZ0.15a: State what is meant by a binary star system.
-
16N.3.SL.TZ0.15b:
(i) Calculate .
(ii) The luminosity of the Sun is 3.8 × 1026 W. Calculate the radius of Alpha Centauri A.
-
16N.3.SL.TZ0.15c:
Show, without calculation, that the radius of Alpha Centauri B is smaller than the radius of Alpha Centauri A.
- 16N.3.SL.TZ0.15d: Alpha Centauri A is in equilibrium at constant radius. Explain how this equilibrium is maintained.
-
16N.3.SL.TZ0.15e:
A standard Hertzsprung–Russell (HR) diagram is shown.
Using the HR diagram, draw the present position of Alpha Centauri A and its expected evolutionary path.
-
16N.3.SL.TZ0.16a:
Determine the distance from Earth to the Cepheid star in parsecs. The luminosity of the Sun is 3.8 × 1026 W. The average apparent brightness of the Cepheid star is 1.1 × 10–9 W m–2.
- 16N.3.SL.TZ0.16b: Explain why Cephids are used as standard candles.
- 16N.3.SL.TZ0.17a: Identify two other characteristics of the CMB radiation that are predicted from the Hot Big Bang...
- 16N.3.SL.TZ0.17b: A spectral line in the hydrogen spectrum measured in the laboratory today has a wavelength of...
-
17M.3.SL.TZ1.9a.i:
State what is meant by a main sequence star.
-
17M.3.SL.TZ1.9a.ii:
Show that the mass of Theta 1 Orionis is about 40 solar masses.
-
17M.3.SL.TZ1.9a.iii:
The surface temperature of the Sun is about 6000 K. Estimate the surface temperature of Theta 1 Orionis.
-
17M.3.SL.TZ1.9a.iv:
Determine the distance of Theta 1 Orionis in AU.
-
17M.3.SL.TZ1.9b:
Discuss how Theta 1 Orionis does not collapse under its own weight.
-
17M.3.SL.TZ1.9c:
The Sun and Theta 1 Orionis will eventually leave the main sequence. Compare and contrast the different stages in the evolution of the two stars.
-
17M.3.SL.TZ1.10a.i:
State two characteristics of the cosmic microwave background (CMB) radiation.
-
17M.3.SL.TZ1.10a.ii:
The present temperature of the CMB is 2.8 K. Calculate the peak wavelength of the CMB.
-
17M.3.SL.TZ1.10b:
Describe how the CMB provides evidence for the Hot Big Bang model of the universe.
-
17M.3.SL.TZ1.10c.i:
Determine the distance to this galaxy using a value for the Hubble constant of H0 = 68 km s–1Mpc–1.
-
17M.3.SL.TZ1.10c.ii:
Estimate the size of the Universe relative to its present size when the light was emitted by the galaxy in (c).
-
17M.3.SL.TZ2.11a:
State the most abundant element in the core and the most abundant element in the outer layer.
-
17M.3.SL.TZ2.11b:
The Hertzsprung–Russell (HR) diagram shows two main sequence stars X and Y and includes lines of constant radius. R is the radius of the Sun.

Using the mass–luminosity relation and information from the graph, determine the ratio .
-
17M.3.SL.TZ2.11c.i:
On the HR diagram in (b), draw a line to indicate the evolutionary path of star X.
-
17M.3.SL.TZ2.11c.ii:
Outline why the neutron star that is left after the supernova stage does not collapse under the action of gravitation.
-
17M.3.SL.TZ2.11c.iii:
The radius of a typical neutron star is 20 km and its surface temperature is 106 K. Determine the luminosity of this neutron star.
-
17M.3.SL.TZ2.11c.iv:
Determine the region of the electromagnetic spectrum in which the neutron star in (c)(iii) emits most of its energy.
-
17M.3.SL.TZ2.12a:
Describe what is meant by the Big Bang model of the universe.
-
17M.3.SL.TZ2.12b:
State two features of the cosmic microwave background (CMB) radiation which are consistent with the Big Bang model.
-
17M.3.SL.TZ2.12c.i:
Determine the distance to the galaxy in Mpc.
-
17M.3.SL.TZ2.12c.ii:
Describe how type Ia supernovae could be used to measure the distance to this galaxy.
- 17N.3.SL.TZ0.12a: State what is meant by a binary star.
-
17N.3.SL.TZ0.12b:
The peak spectral line of Sirius B has a measured wavelength of 115 nm. Show that the surface temperature of Sirius B is about 25 000 K.
-
17N.3.SL.TZ0.12c:
The mass of Sirius B is about the same mass as the Sun. The luminosity of Sirius B is 2.5 % of the luminosity of the Sun. Show, with a calculation, that Sirius B is not a main sequence star.
-
17N.3.SL.TZ0.12d.i:
Determine the radius of Sirius B in terms of the radius of the Sun.
- 17N.3.SL.TZ0.12d.ii: Identify the star type of Sirius B.
- 17N.3.SL.TZ0.12e.i: draw the approximate positions of Sirius A, labelled A and Sirius B, labelled B.
- 17N.3.SL.TZ0.12e.ii: sketch the expected evolutionary path for Sirius A.
- 17N.3.SL.TZ0.13a: Outline one reason for the difference in wavelength.
-
17N.3.SL.TZ0.13b:
Determine the velocity of the galaxy relative to Earth.
-
18M.3.SL.TZ1.10a.i:
Distinguish between the solar system and a galaxy.
-
18M.3.SL.TZ1.10a.ii:
Distinguish between a planet and a comet.
-
18M.3.SL.TZ1.11a.i:
Suggest, using the graphs, why star X is most likely to be a main sequence star.
-
18M.3.SL.TZ1.11a.ii:
Show that the temperature of star X is approximately 10 000 K.
-
18M.3.SL.TZ1.11b.i:
Write down the luminosity of star X (LX) in terms of the luminosity of the Sun (Ls).
-
18M.3.SL.TZ1.11b.ii:
Determine the radius of star X (RX) in terms of the radius of the Sun (Rs).
-
18M.3.SL.TZ1.11b.iii:
Estimate the mass of star X (MX) in terms of the mass of the Sun (Ms).
-
18M.3.SL.TZ1.11c:
Star X is likely to evolve into a stable white dwarf star.
Outline why the radius of a white dwarf star reaches a stable value.
-
18M.3.SL.TZ1.12a:
Explain how international collaboration has helped to refine this value.
-
18M.3.SL.TZ1.12b:
Estimate, in Mpc, the distance between the galaxy and the Earth.
-
18M.3.SL.TZ2.11a:
Main sequence stars are in equilibrium under the action of forces. Outline how this equilibrium is achieved.
-
18M.3.SL.TZ2.11b:
A main sequence star P, is 1.3 times the mass of the Sun. Calculate the luminosity of P relative to the Sun.
-
18M.3.SL.TZ2.11c.i:
The luminosity of the Sun L is 3.85 × 1026 W. Determine the luminosity of Gacrux relative to the Sun.
-
18M.3.SL.TZ2.11c.ii:
The distance to Gacrux can be determined using stellar parallax. Outline why this method is not suitable for all stars.
-
18M.3.SL.TZ2.11d.i:
draw the main sequence.
-
18M.3.SL.TZ2.11d.ii:
plot the position, using the letter P, of the main sequence star P you calculated in (b).
-
18M.3.SL.TZ2.11d.iii:
plot the position, using the letter G, of Gacrux.
-
18M.3.SL.TZ2.11e:
Discuss, with reference to its change in mass, the evolution of star P from the main sequence until its final stable phase.
-
18M.3.SL.TZ2.12a:
Estimate, using the data, the age of the universe. Give your answer in seconds.
-
18M.3.SL.TZ2.12b:
Identify the assumption that you made in your answer to (a).
-
18M.3.SL.TZ2.12c:
On the graph, one galaxy is labelled A. Determine the size of the universe, relative to its present size, when light from the galaxy labelled A was emitted.
- 18N.3.SL.TZ0.11a: Distinguish between a constellation and an open cluster.
- 18N.3.SL.TZ0.11b.i: The parallax angle of Mintaka measured from Earth is 3.64 × 10–3 arc-second. Calculate, in...
- 18N.3.SL.TZ0.11b.ii: State why there is a maximum distance that astronomers can measure using stellar parallax.
-
18N.3.SL.TZ0.12a.i:
Determine the peak wavelength of the radiation emitted by Epsilon Indi.
- 18N.3.SL.TZ0.12a.ii: Using the axis, draw the variation with wavelength of the intensity of the radiation emitted by...
-
18N.3.SL.TZ0.12a.iii:
The following data are available for the Sun.
Surface temperature = 5800 K
Luminosity =
Mass =
Radius =
Epsilon Indi has a radius of 0.73 . Show that the luminosity of Epsilon Indi is 0.2 .
-
18N.3.SL.TZ0.12b:
Epsilon Indi is a main sequence star. Show that the mass of Epsilon Indi is 0.64 .
- 18N.3.SL.TZ0.12c: Describe how the chemical composition of a star may be determined.
- 18N.3.SL.TZ0.12d: Describe the stages in the evolution of Epsilon Indi from the point when it leaves the main...
-
18N.3.SL.TZ0.13a:
Outline how Hubble measured the recessional velocities of galaxies.
-
18N.3.SL.TZ0.13b:
Using the graph, determine in s, the age of the universe.
- 18N.3.HL.TZ0.17a: Distinguish between a constellation and an open cluster.
- 18N.3.HL.TZ0.17b.i: The parallax angle of Mintaka measured from Earth is 3.64 × 10–3 arc-second. Calculate, in...
- 18N.3.HL.TZ0.17b.ii: State why there is a maximum distance that astronomers can measure using stellar parallax.
-
18N.3.HL.TZ0.18a.i:
Determine the peak wavelength of the radiation emitted by Epsilon Indi.
- 18N.3.HL.TZ0.18a.ii: Using the axis, draw the variation with wavelength of the intensity of the radiation emitted by...
-
18N.3.HL.TZ0.18a.iii:
The following data are available for the Sun.
Surface temperature = 5800 K
Luminosity =
Mass =
Radius =
Epsilon Indi has a radius of 0.73 . Show that the luminosity of Epsilon Indi is 0.2 .
-
18N.3.HL.TZ0.18b:
Epsilon Indi is a main sequence star. Show that the mass of Epsilon Indi is 0.64 .
-
18N.3.HL.TZ0.18c:
The Sun will spend about nine billion years on the main sequence. Calculate how long Epsilon Indi will spend on the main sequence.
- 18N.3.HL.TZ0.18d: Describe the stages in the evolution of Epsilon Indi from the point when it leaves the main...
-
18N.3.HL.TZ0.19a:
Outline how Hubble measured the recessional velocities of galaxies.
-
18N.3.HL.TZ0.19b:
Use the graph to determine the age of the universe in s.
- 19M.3.SL.TZ2.13ai: Outline the processes that produce the change of luminosity with time of Cepheid variables.
- 19M.3.SL.TZ2.13aii: Explain how Cepheid variables are used to determine distances.
-
19M.3.SL.TZ2.13bi:
Determine the peak apparent brightness of δ-Cephei as observed from Earth.
-
19M.3.SL.TZ2.13bii:
Calculate the peak surface temperature of δ-Cephei.
- 19M.3.SL.TZ2.14ai: A galaxy is 1.6 × 108 ly from Earth. Show that its recessional speed as measured from Earth is...
-
19M.3.SL.TZ2.14aii:
A line in the hydrogen spectrum when measured on Earth has a wavelength of 486 nm. Calculate, in nm, the wavelength of the same hydrogen line when observed in the galaxy’s emission spectrum.
- 19M.3.SL.TZ2.14b: Outline how observations of spectra from distant galaxies provide evidence that the universe is...
- 19M.3.SL.TZ2.15a: Identify, on the HR diagram, the position of the Sun. Label the position S.
- 19M.3.SL.TZ2.15b: Suggest the conditions that will cause the Sun to become a red giant.
-
19M.3.SL.TZ2.15c:
Outline why the Sun will maintain a constant radius after it becomes a white dwarf.
-
19M.3.SL.TZ2.15d:
During its evolution, the Sun is likely to be a red giant of surface temperature 3000 K and luminosity 104 L☉. Later it is likely to be a white dwarf of surface temperature 10 000 K and luminosity 10-4 L☉. Calculate the .
- 19M.3.HL.TZ1.19b: Suggest why type I a supernovae were used in the study that led to the conclusion that the...
- 19N.3.SL.TZ0.10 a: Distinguish between a constellation and a stellar cluster.
-
19N.3.SL.TZ0.10b(i):
The peak wavelength of radiation from Eta Cassiopeiae A is 490 nm. Show that the surface temperature of Eta Cassiopeiae A is about 6000 K.
-
19N.3.SL.TZ0.10b(ii):
The surface temperature of Eta Cassiopeiae B is 4100 K. Determine the ratio .
-
19N.3.SL.TZ0.10b(iii):
The distance of the Eta Cassiopeiae system from the Earth is 1.8 × 1017 m. Calculate, in terms of , the luminosity of Eta Cassiopeiae A.
- 19N.3.SL.TZ0.10c(i): On the HR diagram, draw the present position of Eta Cassiopeiae A.
- 19N.3.SL.TZ0.10c(ii): State the star type of Eta Cassiopeiae A.
-
19N.3.SL.TZ0.10c(iii):
Calculate the ratio .
-
19N.3.SL.TZ0.10c(iv):
Deduce the final evolutionary state of Eta Cassiopeiae A.
- 19N.3.SL.TZ0.11a(i): Outline how the light spectra of distant galaxies are used to confirm hypotheses about the...
-
19N.3.SL.TZ0.11a(ii):
Light from a hydrogen source in a laboratory on Earth contains a spectral line of wavelength 122 nm. Light from the same spectral line reaching Earth from a distant galaxy has a wavelength of 392 nm. Determine the ratio of the present size of the universe to the size of the universe when the light was emitted by the galaxy.
-
19N.3.SL.TZ0.11b(i):
Estimate the age of the universe in seconds using the Hubble constant H0 = 70 km s–1 Mpc–1.
-
19N.3.SL.TZ0.11b(ii):
Outline why the estimate made in (b)(i) is unlikely to be the actual age of the universe.
- 19N.3.HL.TZ0.16a(i): Outline how the light spectra of distant galaxies are used to confirm hypotheses about the...
-
19N.3.HL.TZ0.16a(ii):
Light from a hydrogen source in a laboratory on Earth contains a spectral line of wavelength 122 nm. Light from the same spectral line reaching Earth from a distant galaxy has a wavelength of 392 nm. Determine the ratio of the present size of the universe to the size of the universe when the light was emitted by the galaxy.
- 19N.3.SL.TZ0.10a: Distinguish between a constellation and a stellar cluster.
-
20N.3.SL.TZ0.14a:
The astronomical unit () and light year () are convenient measures of distance in astrophysics. Define each unit.
:
:
- 20N.3.SL.TZ0.14b(i): Comets develop a tail as they approach the Sun. Identify one other characteristic of comets.
- 20N.3.SL.TZ0.14b(ii): Identify one object visible in the image that is outside our Solar System.
-
20N.3.SL.TZ0.15a:
Show that the apparent brightness , where is the distance of the object from Earth, is the surface temperature of the object and is the surface area of the object.
-
20N.3.SL.TZ0.15b:
Two of the brightest objects in the night sky seen from Earth are the planet Venus and the star Sirius. Explain why the equation is applicable to Sirius but not to Venus.
-
20N.3.SL.TZ0.16a:
The light from a distant galaxy shows that .
Calculate the ratio .
-
20N.3.SL.TZ0.16b:
Outline how Hubble’s law is related to .
-
20N.3.SL.TZ0.17a:
Show by calculation that Eta Aquilae A is not on the main sequence.
-
20N.3.SL.TZ0.17b(i):
Estimate, in , the distance to Eta Aquilae A using the parallax angle in the table.
-
20N.3.SL.TZ0.17b(ii):
Estimate, in , the distance to Eta Aquilae A using the luminosity in the table, given that .
- 20N.3.SL.TZ0.17d: Eta Aquilae A is a Cepheid variable. Explain why the brightness of Eta Aquilae A varies.
-
20N.3.HL.TZ0.21a:
The light from a distant galaxy shows that .
Calculate the ratio .
-
20N.3.HL.TZ0.21b:
Outline how Hubble’s law is related to .
-
20N.3.HL.TZ0.22a:
Show by calculation that Eta Aquilae A is not on the main sequence.
-
20N.3.HL.TZ0.22b(i):
Estimate, in , the distance to Eta Aquilae A using the parallax angle in the table.
-
20N.3.HL.TZ0.22b(ii):
Estimate, in , the distance to Eta Aquilae A using the luminosity in the table, given that .
- 20N.3.HL.TZ0.22d: Eta Aquilae A is a Cepheid variable. Explain why the brightness of Eta Aquilae A varies.
- 21N.1.SL.TZ0.30: Which is correct for a black-body radiator? A. The power it emits from a unit surface area...
Option D: Astrophysics (Additional higher level option topics)
- 16N.3.HL.TZ0.24a: Describe how some white dwarf stars become type Ia supernovae.
- 16N.3.HL.TZ0.24b: Hence, explain why a type Ia supernova is used as a standard candle.
- 16N.3.HL.TZ0.24c: Explain how the observation of type Ia supernovae led to the hypothesis that dark energy exists.
-
16N.3.HL.TZ0.25a:
Calculate the rotation velocity of stars 4.0 kpc from the centre of the galaxy. The average density of the galaxy is 5.0 × 10–21 kg m–3.
- 16N.3.HL.TZ0.25b: Explain why the rotation curves are evidence for the existence of dark matter.
-
17M.3.HL.TZ1.16a:
Outline, with reference to star formation, what is meant by the Jeans criterion.
-
17M.3.HL.TZ1.16b:
In the proton–proton cycle, four hydrogen nuclei fuse to produce one nucleus of helium releasing a total of 4.3 × 10–12 J of energy. The Sun will spend 1010 years on the main sequence. It may be assumed that during this time the Sun maintains a constant luminosity of 3.8 × 1026 W.
Show that the total mass of hydrogen that is converted into helium while the Sun is on the main sequence is 2 × 1029 kg. -
17M.3.HL.TZ1.16c:
Massive stars that have left the main sequence have a layered structure with different chemical elements in different layers. Discuss this structure by reference to the nuclear reactions taking place in such stars.
-
17M.3.HL.TZ1.17a:
The graph shows the variation with time t of the cosmic scale factor R in the flat model of the universe in which dark energy is ignored.

On the axes above draw a graph to show the variation of R with time, when dark energy is present.
-
17M.3.HL.TZ1.17b.i:
The density of the observable matter in the universe is only 0.05 ρc. Suggest how the remaining 0.27 ρc is accounted for.
-
17M.3.HL.TZ1.17b.ii:
The density of dark energy is ρΛc2 where ρΛ = ρc – ρm. Calculate the amount of dark energy in 1 m3 of space.
-
17M.3.HL.TZ2.19a.i:
Derive, using the concept of the cosmological origin of redshift, the relation
T
between the temperature T of the cosmic microwave background (CMB) radiation and the cosmic scale factor R.
-
17M.3.HL.TZ2.19a.ii:
The present temperature of the CMB is 2.8 K. This radiation was emitted when the universe was smaller by a factor of 1100. Estimate the temperature of the CMB at the time of its emission.
-
17M.3.HL.TZ2.19b:
State how the anisotropies in the CMB distribution are interpreted.
-
17M.3.HL.TZ2.20a:
Describe what is meant by dark matter.
-
17M.3.HL.TZ2.20b:
The distribution of mass in a spherical system is such that the density ρ varies with distance r from the centre as
ρ =
where k is a constant.
Show that the rotation curve of this system is described by
v = constant.
-
17M.3.HL.TZ2.20c:
Curve A shows the actual rotation curve of a nearby galaxy. Curve B shows the predicted rotation curve based on the visible stars in the galaxy.
Explain how curve A provides evidence for dark matter.
-
17N.3.HL.TZ0.20a:
The Sun is a second generation star. Outline, with reference to the Jeans criterion (MJ), how the Sun is likely to have been formed.
-
17N.3.HL.TZ0.20b:
Suggest how fluctuations in the cosmic microwave background (CMB) radiation are linked to the observation that galaxies collide.
-
17N.3.HL.TZ0.20c:
Show that the critical density of the universe is
where H is the Hubble parameter and G is the gravitational constant.
-
18M.3.HL.TZ1.18a:
Describe the formation of a type Ia supernova.
-
18M.3.HL.TZ1.18b.i:
Show that the distance to the supernova is approximately 3.1 × 1018 m.
-
18M.3.HL.TZ1.18b.ii:
State one assumption made in your calculation.
-
18M.3.HL.TZ1.19a:
The mass of visible matter in the galaxy is M.
Show that for stars where r > R0 the velocity of orbit is v = .
-
18M.3.HL.TZ1.19b:
Draw on the axes the observed variation with r of the orbital speed v of stars in a galaxy.
-
18M.3.HL.TZ1.19c:
Explain, using the equation in (a) and the graphs, why the presence of visible matter alone cannot account for the velocity of stars when r > R0.
-
18M.3.HL.TZ2.18a:
Outline, with reference to the Jeans criterion, why a cold dense gas cloud is more likely to form new stars than a hot diffuse gas cloud.
-
18M.3.HL.TZ2.18b:
Explain how neutron capture can produce elements with an atomic number greater than iron.
-
18M.3.HL.TZ2.19a:
Explain the evidence that indicates the location of dark matter in galaxies.
-
18M.3.HL.TZ2.19b:
Outline why a hypothesis of dark energy has been developed.
- 18N.3.HL.TZ0.17c: The Great Nebula is located in Orion. Describe, using the Jeans criterion, the...
- 18N.3.HL.TZ0.20a: Outline what is meant by dark energy.
- 18N.3.HL.TZ0.20b: State two candidates for dark matter.
-
18N.3.HL.TZ0.21a:
Show that the temperature of the universe is inversely proportional to the cosmic scale factor.
-
18N.3.HL.TZ0.21b:
The present temperature of the cosmic microwave background (CMB) radiation is 3 K. Estimate the size of the universe relative to the present size of the universe when the temperature of the CMB was 300 K.
- 19M.3.HL.TZ2.21b: Describe the r process which occurs during type II supernovae nucleosynthesis.
- 19M.3.HL.TZ1.19a.i: Describe the mechanism of formation of type I a supernovae.
-
19M.3.HL.TZ1.19a.ii:
Describe the mechanism of formation of type II supernovae.
- 19M.3.HL.TZ1.20a: Light from distant galaxies is redshifted. Explain the cosmological origin of this redshift.
- 19M.3.HL.TZ1.20b.i: Draw, on the axes, a graph to show the variation with time of the cosmic scale factor R for the...
-
19M.3.HL.TZ1.20b.ii:
Compare and contrast, the variation with time of the temperature of the cosmic background (CMB) radiation, for the two models from the present time onward.
- 19M.3.HL.TZ2.21a: Explain the formation of a type I a supernova which enables the star to be used as a standard...
-
19M.3.HL.TZ2.22a:
Justify that the total energy of this particle is .
-
19M.3.HL.TZ2.22b:
At critical density there is zero total energy. Show that the critical density of the universe is: .
- 19M.3.HL.TZ2.22c: The accepted value for the Hubble constant is 2.3 × 10−18 s−1. Estimate the critical density of...
- 19N.3.HL.TZ0.16b(i): State what is meant by the critical density.
-
19N.3.HL.TZ0.16b(ii):
Calculate the density of matter in the universe, using the Hubble constant 70 km s–1 Mpc–1.
- 19N.3.HL.TZ0.16b(iii): It is estimated that less than 20 % of the matter in the universe is observable. Discuss how...
-
19N.3.HL.TZ0.17a:
Proxima Centauri is a main sequence star with a mass of 0.12 solar masses.
Estimate .
- 19N.3.HL.TZ0.17b: Describe why iron is the heaviest element that can be produced by nuclear fusion processes inside...
-
19N.3.HL.TZ0.17c:
Discuss one process by which elements heavier than iron are formed in stars.
- 20N.3.HL.TZ0.21c: Hubble originally linked galactic redshift to a Doppler effect arising from galactic recession....
- 20N.3.HL.TZ0.22e: Eta Aquilae A was on the main sequence before it became a variable star. Compare, without...
- 20N.3.HL.TZ0.23: In 2017, two neutron stars were observed to merge, forming a black hole. The material released...
- 20N.3.HL.TZ0.24a: State the nature of the anisotropies observed in the CMB radiation.
-
20N.3.HL.TZ0.24b:
Identify two possible causes of the anisotropies in (a).
- 21N.1.SL.TZ0.30: Which is correct for a black-body radiator? A. The power it emits from a unit surface area...
