DP Physics Questionbank

A.5 – General relativity (HL only)
| Path: |
Description
Nature of science:
Creative and critical thinking: Einstein’s great achievement, the general theory of relativity, is based on intuition, creative thinking and imagination, namely to connect the geometry of spacetime (through its curvature) to the mass and energy content of spacetime. For years it was thought that nothing could escape a black hole and this is true but only for classical black holes. When quantum theory is taken into account a black hole radiates like a black body. This unexpected result revealed other equally unexpected connections between black holes and thermodynamics. (1.4)
Understandings:
- The equivalence principle
- The bending of light
- Gravitational redshift and the Pound–Rebka–Snider experiment
- Schwarzschild black holes
- Event horizons
- Time dilation near a black hole
- Applications of general relativity to the universe as a whole
Applications and skills:
- Using the equivalence principle to deduce and explain light bending near massive objects
- Using the equivalence principle to deduce and explain gravitational time dilation
- Calculating gravitational frequency shifts
- Describing an experiment in which gravitational redshift is observed and measured
- Calculating the Schwarzschild radius of a black hole
- Applying the formula for gravitational time dilation near the event horizon of a black hole
Guidance:
- Students should recognize the equivalence principle in terms of accelerating reference frames and freely falling frames
Data booklet reference:
Theory of knowledge:
- Although Einstein self-described the cosmological constant as his “greatest blunder”, the 2011 Nobel Prize was won by scientists who had proved it to be valid through their studies on dark energy. What other examples are there of initially doubted claims being proven correct later in history?
Utilization:
- For the global positioning system to be so accurate, general relativity must be taken into account in calculating the details of the satellite’s orbit
- The development of the general theory of relativity has been used to explain the very large-scale behaviour of the universe as a whole with far-reaching implications about the future development and fate of the universe
Aims:
- Aim 2: the general theory of relativity is a great synthesis of ideas that are required to describe the large-scale structure of the universe
- Aim 9: it must be appreciated that the magnificent Newtonian structure had serious limitations when it came to the description of very detailed aspects of planetary motion
Directly related questions
-
16N.3.HL.TZ0.9b:
Suggest, whether your answer to (a) underestimates or overestimates the correction required to the time signal.
-
16N.3.HL.TZ0.9a:
The gravitational field strength at 20 Mm above the surface of the Earth is about 0.6 N kg–1. Estimate the time correction per day needed to the time signals, due to the gravitational redshift.
-
17M.3.HL.TZ2.7a.i:
State what is meant by the event horizon of a black hole.
-
17M.3.HL.TZ1.6b:
Explain whether the detected frequency would be greater or less than the emitted frequency.
-
17M.3.HL.TZ2.7a.iii:
Suggest why the surface area of the event horizon can never decrease.
-
17M.3.HL.TZ1.6a:
Calculate the expected shift in frequency between the emitted and the detected gamma rays.
-
17M.3.HL.TZ2.7a.ii:
Show that the surface area A of the sphere corresponding to the event horizon is given by
.
-
17M.3.HL.TZ2.7b:
The diagram shows a box that is falling freely in the gravitational field of a planet.
A photon of frequency f is emitted from the floor of the box and is received at the ceiling. State and explain the frequency of the photon measured at the ceiling.
-
20N.3.HL.TZ0.7b(ii):
Explain the cause of the frequency shift for the gamma rays in your answer in (a) if the tower and detector were accelerating towards the gamma rays in free space.
-
20N.3.HL.TZ0.7b(i):
Explain the cause of the frequency shift for the gamma rays in your answer in (a) in the Earth’s gravitational field.
-
20N.3.HL.TZ0.7a:
Calculate the fractional change in frequency of the gamma rays at the detector.
-
17N.3.HL.TZ0.8a:
Outline why the clock near the black hole runs slowly compared to a clock close to the distant observer.
-
17N.3.HL.TZ0.8b:
Calculate the number of ticks detected in 10 ks by the distant observer.
-
18M.3.HL.TZ1.7c:
Observer A now sends a beam of light initially parallel to the surface of the planet.
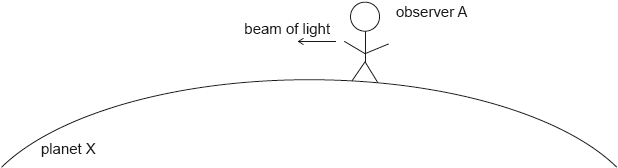
Explain why the path of the light is curved.
-
18M.3.HL.TZ1.7a:
Calculate the shift in frequency observed by A in terms of Δf.
-
18M.3.HL.TZ1.7b:
Calculate the gravitational field strength on the surface of planet X.
The following data is given:
Δf = 170 Hz.
The distance between observer A and B is 10 km.
-
18M.3.HL.TZ2.7a.i:
Outline what is meant by the event horizon of a black hole.
-
18M.3.HL.TZ2.7a.ii:
Calculate the distance of the event horizon of the black hole from its centre.
Mass of Sun = 2 × 1030 kg
-
18M.3.HL.TZ2.7b:
Star S-2 is in an elliptical orbit around a black hole. The distance of S-2 from the centre of the black hole varies between a few light-hours and several light-days. A periodic event on S-2 occurs every 5.0 s.
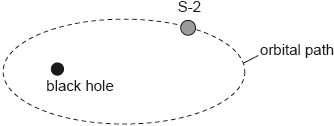
Discuss how the time for the periodic event as measured by an observer on the Earth changes with the orbital position of S-2.
- 18N.3.HL.TZ0.7a.i: State what is meant by the event horizon of a black hole.
-
18N.3.HL.TZ0.7a.ii:
The mass of the black hole is 4.0 × 1036 kg. Calculate the Schwarzschild radius of the black hole.
-
18N.3.HL.TZ0.7b:
The probe is stationary above the event horizon of the black hole in (a). The probe sends a radio pulse every 1.0 seconds (as measured by clocks on the probe). The spacecraft receives the pulses every 2.0 seconds (as measured by clocks on the spacecraft). Determine the distance of the probe from the centre of the black hole.
- 19M.3.HL.TZ1.7b.i: State and explain the path of the light ray according to observer X.
- 19M.3.HL.TZ1.7a: State the equivalence principle.
- 19M.3.HL.TZ1.7b.ii: State and explain the path of the light ray according to observer Y.
- 19M.3.HL.TZ2.9b: Calculate the frequency change.
- 19M.3.HL.TZ2.9a: Explain why a change in frequency is expected for the photon detected at the top of the rocket.
-
19N.3.HL.TZ0.6a:
Explain why the frequency of the radio waves detected by the observer is lower than .
-
19N.3.HL.TZ0.6b:
The probe emits 20 short pulses of these radio waves every minute, according to a clock in the probe. Calculate the time between pulses as measured by the observer.
