A satellite in a circular orbit around the Earth needs to reduce its orbital radius.

What is the work done by the satellite rocket engine and the change in kinetic energy resulting from this shift in orbital height?

Calculate the electric potential at O.

Determine whether the object will reach the surface of the sphere.

The electric potential at a point a distance 2.8 m from the centre of the sphere is 7.71 kV. Determine the radius of the sphere.

The gravitational potential due to the Sun at a distance r from its centre is V_S. Show that

rV_S = constant.

Two point charges Q₁ and Q₂ are one metre apart. The graph shows the variation of electric potential V with distance $x$ from Q₁.

What is $\frac{Q_1}{Q_2}$?

A.   $\frac{1}{16}$

B.   $\frac{1}{4}$

C.   4

D.   16

Show that the speed $v$ of the electron with mass $m$, is given by $v=\sqrt{\frac{2k{e}^2}{mr}}$.

Predict the charge on each sphere.

State the maximum distance between the centres of the nuclei for which the production of ${}_{15}^{32}\text{P}$ is likely to occur.

The following data for the Mars–Phobos system and the Earth–Moon system are available:

Mass of Earth = 5.97 × 10²⁴ kg

The Earth–Moon distance is 41 times the Mars–Phobos distance.

The orbital period of the Moon is 86 times the orbital period of Phobos.

Calculate, in kg, the mass of Mars.

The escape speed for the Earth is $v$_esc. Planet X has half the density of the Earth and twice the radius. What is the escape speed for planet X?

A.   $\frac{v_{\text{esc}}}{2}$

B.   $\frac{v_{\text{esc}}}{\sqrt{2}}$

C.  $v$_esc

D.   $\sqrt{2}$ $v$_esc

The escape velocity for an object at the surface of the Earth is v_esc. The diameter of the Moon is 4 times smaller than that of the Earth and the mass of the Moon is 81 times smaller than that of the Earth. What is the escape velocity of the object on the Moon?

A. $\frac{2}{81}$v_esc

B. $\frac{4}{81}$v_esc

C. $\frac{2}{9}$v_esc

D. $\frac{4}{9}$v_esc

The diagram shows the path of an asteroid as it moves past the planet.

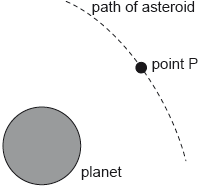
When the asteroid was far away from the planet it had negligible speed. Estimate the speed of the asteroid at point P as defined in (b).

Suppose the star could contract to half its original radius without any loss of mass. Discuss the effect, if any, this has on the total energy of the planet.

The graph shows the variation of the gravitational potential V with distance r from the centre of a uniform spherical planet. The radius of the planet is R. The shaded area is S.

What is the work done by the gravitational force as a point mass m is moved from the surface of the planet to a distance 6R from the centre?

A. m (V2 – V1 )

B. m (V1 – V2 )

C. mS

D. S

Explain what is meant by the gravitational potential at the surface of a planet.

Show that the $\frac{\mathrm{gravitational} \mathrm{potential} \mathrm{due} \mathrm{to} \mathrm{Jupiter} \mathrm{at} \mathrm{the} \mathrm{orbit} \mathrm{of} \mathrm{Io}}{ \mathrm{gravitational} \mathrm{potential} \mathrm{due} \mathrm{to} \mathrm{Io} \mathrm{at} \mathrm{the} \mathrm{surface} \mathrm{of} \mathrm{Io}}$ is about 80.

Satellite X is in orbit around the Earth. An identical satellite Y is in a higher orbit. What is correct for the total energy and the kinetic energy of the satellite Y compared with satellite X?

An electron of mass m_e orbits an alpha particle of mass m_α in a circular orbit of radius r. Which expression gives the speed of the electron?

A.     $\sqrt{\frac{2k{e}^2}{m_{e}r}}$

B.     $\sqrt{\frac{2k{e}^2}{m_{a}r}}$

C.     $\sqrt{\frac{4k{e}^2}{m_{e}r}}$

D.     $\sqrt{\frac{4k{e}^2}{m_{a}r}}$

The gravitational potential is $V$ at a distance $R$ above the surface of a spherical planet of radius $R$ and uniform density. What is the gravitational potential a distance $2R$ above the surface of the planet?

A. $\frac{V}{4}$

B. $\frac{4V}{9}$

C. $\frac{V}{2}$

D. $\frac{2V}{3}$

Hence, deduce that the total energy of the electron is given by $E_{\mathrm{TOT}}=-\frac{k{e}^2}{r}$.

The orbital period T of a moon orbiting a planet of mass M is given by

$$\frac{R^3}{T^2}=kM$$

where R is the average distance between the centre of the planet and the centre of the moon.

Show that $k=\frac{G}{4{\pi }^2}$

The force acting between two point charges is $F$ when the separation of the charges is $x$. What is the force between the charges when the separation is increased to $3x$?

A. $\frac{F}{3}$

B. $\frac{F}{3x^2}$

C. $\frac{F}{9}$

D. $\frac{F}{9x^2}$

A satellite orbits planet $\text{X}$ with a speed $v_{\text{X}}$ at a distance $\text{r}$ from the centre of planet $\text{X}$. Another satellite orbits planet $\text{Y}$ at a speed of $v_{\text{y}}$ at a distance $\text{r}$ from the centre of planet $\text{Y}$. The mass of planet $\text{X}$ is $M$ and the mass of planet $\text{Y}$ is $4M$. What is the ratio of $\frac{v_{\text{X}}}{v_{\text{y}}}$?

A.  0.25

B.  0.5

C.  2.0

D.  4.0

Determine the charge $Q$ of the sphere.

Estimate the escape speed of the spacecraft from the planet–star system.

Determine, in J, the minimum initial kinetic energy that the deuterium nucleus must have in order to produce ${}_{15}^{32}\text{P}$. Assume that the phosphorus nucleus is stationary throughout the interaction and that only electrostatic forces act.

Outline, without calculation, whether or not the electric potential at P is zero.

Draw, on the axes, the variation of electric potential $V$ with distance $r$ from the centre of the sphere.

Outline, using (b)(i), why it is not correct to use the equation $\sqrt{\frac{2G\times \text{mass of Io}}{\text{radius of Io}}}$ to calculate the speed required for the spacecraft to reach infinity from the surface of $\text{Io}$.

Explain why the electric potential decreases from A to B.

An unpowered projectile is fired vertically upwards into deep space from the surface of planet Venus. Assume that the gravitational effects of the Sun and the other planets are negligible.

The following data are available.

(i) Determine the initial kinetic energy of the projectile.

(ii) Describe the subsequent motion of the projectile until it is effectively beyond the gravitational field of Venus.

Satellite X orbits 6600 km from the centre of the Earth.

Mass of the Earth = 6.0 x 10²⁴ kg

Show that the orbital speed of satellite X is about 8 km s^–1.

A spacecraft moves towards the Earth under the influence of the gravitational field of the Earth.

The three quantities that depend on the distance r of the spacecraft from the centre of the Earth are the

I.   gravitational potential energy of the spacecraft
II   gravitational field strength acting on the spacecraft
III. gravitational force acting on the spacecraft.

Which of the quantities are proportional to $\frac{1}{r^2}$?

A. I and II only

B. I and III only

C. II and III only

D. I, II and III

In this model the electron loses energy by emitting electromagnetic waves. Describe the predicted effect of this emission on the orbital radius of the electron.

Show that the total energy of the planet is given by the equation shown.

$E=\frac{1}{2}mV$

Calculate the gravitational potential energy of the Earth in its orbit around the Sun. Give your answer to an appropriate number of significant figures.

Calculate the total energy of the Earth in its orbit.

A meteorite, very far from planet X begins to fall to the surface with a negligibly small initial speed. The mass of planet X is 3.1 × 10²¹ kg and its radius is 1.2 × 10⁶ m. The planet has no atmosphere. Calculate the speed at which the meteorite will hit the surface.

The mass of the Earth is M_E and the mass of the Moon is M_M. Their respective radii are R_E and R_M.

Which is the ratio $\frac{\text{escape speed from the Earth}}{\text{escape speed from the Moon}}$?

A.     $\sqrt{\frac{M_{\text{M}}{R}_{\text{M}}}{M_{\text{E}}{R}_{\text{E}}}}$

B.     $\sqrt{\frac{M_{\text{E}}{R}_{\text{E}}}{M_{\text{M}}{R}_{\text{M}}}}$

C.     $\sqrt{\frac{M_{\text{E}}{R}_{\text{M}}}{M_{\text{M}}{R}_{\text{E}}}}$

D.     $\sqrt{\frac{M_{\text{M}}{R}_{\text{E}}}{M_{\text{E}}{R}_{\text{M}}}}$

The escape speed from a planet of radius R is v_esc. A satellite orbits the planet at a distance R from the surface of the planet. What is the orbital speed of the satellite?

A. $\frac{1}{2}{v}_{\text{esc}}$

B. $\frac{\sqrt{2}}{2}{v}_{\text{esc}}$

C. $\sqrt{2}{v}_{\text{esc}}$

D. $2v_{\text{esc}}$

An engineer needs to move a space probe of mass 3600 kg from Ganymede to Callisto. Calculate the energy required to move the probe from the orbital radius of Ganymede to the orbital radius of Callisto. Ignore the mass of the moons in your calculation. 

Discuss, by reference to the answer in (b), whether it is likely that Titan will lose its atmosphere of nitrogen.

A satellite of mass $m$ orbits a planet of mass $M$ in a circular orbit of radius $r$. What is the work that must be done on the satellite to increase its orbital radius to $2r$?

A.  $\frac{GMm}{r}$

B.  $\frac{GMm}{2r}$

C.  $\frac{GMm}{4r}$

D.  $\frac{GMm}{8r}$

The mass of Titan is 0.025 times the mass of the Earth and its radius is 0.404 times the radius of the Earth. The escape speed from Earth is 11.2 km s⁻¹. Show that the escape speed from Titan is 2.8 km s⁻¹.

Show that the charge on the surface of the sphere is +18 μC.

An object of mass $m$ is launched from the surface of the Earth. The Earth has a mass $M$ and radius $r$. The acceleration due to gravity at the surface of the Earth is $g$. What is the escape speed of the object from the surface of the Earth?

A.  $\sqrt{gr}$

B.  $\sqrt{2gr}$

C.  $\sqrt{2Mgr}$

D.  $\sqrt{2mgr}$