| Date | November 2017 | Marks available | 1 | Reference code | 17N.1.HL.TZ0.28 |
| Level | Higher level | Paper | Paper 1 | Time zone | 0 - no time zone |
| Command term | Question number | 28 | Adapted from | N/A |
Question
Monochromatic light is incident on two identical slits to produce an interference pattern on a screen. One slit is then covered so that no light emerges from it. What is the change to the pattern observed on the screen?
A. Fewer maxima will be observed.
B. The intensity of the central maximum will increase.
C. The outer maxima will become narrower.
D. The width of the central maximum will decrease.
Markscheme
A
Examiners report
Syllabus sections
-
18M.2.HL.TZ2.5c:
The slit separation is increased. Outline one change observed on the screen.
-
18M.2.HL.TZ2.5a:
Monochromatic light from two identical lamps arrives on a screen.
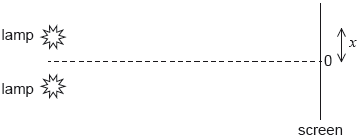
The intensity of light on the screen from each lamp separately is I0.
On the axes, sketch a graph to show the variation with distance x on the screen of the intensity I of light on the screen.
-
22M.1.HL.TZ2.30:
In two different experiments, white light is passed through a single slit and then is either refracted through a prism or diffracted with a diffraction grating. The prism produces a band of colours from M to N. The diffraction grating produces a first order spectrum P to Q.
What are the colours observed at M and P?
- 19M.1.HL.TZ1.29: In a Young’s double-slit experiment, the distance between fringes is too small to be...
- 17M.2.HL.TZ2.4c.ii: Suggest the variation in the output voltage from the light sensor that will be observed as...
- 16N.1.HL.TZ0.27: Monochromatic light is incident on a double slit. Both slits have a finite width. The light...
-
17M.2.HL.TZ2.4c.i:
Determine the width of one of the slits.
- 18N.1.HL.TZ0.27: The graph shows the variation with diffraction angle of the intensity of light...
-
18N.1.HL.TZ0.28:
A beam of monochromatic light is incident normally on a diffraction grating. The grating spacing is d. The angles between the different orders are shown on the diagram.
What is the expression for the wavelength of light used?
A.
B.
C. d sin α
D. d sin β
- 18N.2.HL.TZ0.5b.iii: The light source is changed so that white light is incident on the diffraction grating....
- 18N.2.HL.TZ0.5b.ii: Calculate the angle between the first-order line of the red light in the hydrogen spectrum...
-
21N.1.HL.TZ0.28:
Monochromatic light of wavelength in air is incident normally on a thin liquid film of refractive index that is suspended in air. The rays are shown at an angle to the normal for clarity.
What is the minimum thickness of the film so that the reflected light undergoes constructive interference?
A.B.
C.
D.
- 21N.2.HL.TZ0.8d.iii: State what will happen to the intensity of the secondary maxima.
- 21N.2.HL.TZ0.8d.ii: State what will happen to the width of the primary maxima.
- 19N.2.HL.TZ0.10b(i): state, in terms of d, the path difference between the reflected rays X and Y.
- 17M.1.HL.TZ1.27: For fringes to be observed in a double-slit interference experiment, the slits must emit...
- 19M.2.HL.TZ2.8ci: Suggest why, after this change, the intensity at P will be less than that at M.
-
19M.1.HL.TZ1.31:
A transparent liquid film of refractive index 1.5 coats the outside of a glass lens of higher refractive index. The liquid film is used to eliminate reflection from the lens at wavelength λ in air.
What is the minimum thickness of the liquid film coating and the phase change at the liquid–glass interface?
-
17N.1.HL.TZ0.29:
A transparent liquid forms a parallel-sided thin film in air. The diagram shows a ray I incident on the upper air–film boundary at normal incidence (the rays are shown at an angle to the normal for clarity).
Reflections from the top and bottom surfaces of the film result in three rays J, K and L. Which of the rays has undergone a phase change of rad?
A. J only
B. J and L only
C. J and K only
D. J, K and L
-
17N.2.HL.TZ0.6a.i:
Explain why zero intensity is observed at position A.
-
19N.2.HL.TZ0.10a:
Predict whether reflected ray X undergoes a phase change.
- 18M.1.HL.TZ1.28: Monochromatic light is incident on 4 rectangular, parallel slits. The first principal maximum...
-
18M.2.HL.TZ1.3b.i:
Calculate the angular separation between the central peak and the missing peak in the double-slit interference intensity pattern. State your answer to an appropriate number of significant figures.
-
19N.1.HL.TZ0.28:
Light of wavelength λ is normally incident on a diffraction grating of spacing 3λ. What is the angle between the two second-order maxima?
A.
B.
C.
D. >90° so no second orders appear
-
17N.2.HL.TZ0.6b.i:
State and explain the differences between the pattern on the screen due to the grating and the pattern due to the double slit.
- 19N.2.HL.TZ0.10b(iii): discuss a practical advantage of this arrangement.
-
18M.1.HL.TZ1.27:
Monochromatic light of wavelength λ in air is incident normally on a thin film of refractive index n. The film is surrounded by air. The intensity of the reflected light is a minimum. What is a possible thickness of the film?
A.
B.
C.
D.
-
16N.1.HL.TZ0.28:
Light of wavelength λ is incident normally on a diffraction grating that has a slit separation of . What is the greatest number of maxima that can be observed using this arrangement?
A. 4
B. 6
C. 7
D. 9 - 20N.1.HL.TZ0.29: White light is incident normally on separate diffraction gratings X and Y. Y has a greater...
-
21M.2.HL.TZ1.6a:
State the phase change when a ray is reflected at B.
- 21M.2.HL.TZ1.6c.i: State the Rayleigh criterion for resolution.
-
21M.2.HL.TZ1.6b:
Explain the condition for w that eliminates reflection for a particular light wavelength in air .
- 21M.2.HL.TZ2.8a.ii: State, in terms of λ, the path length between points X and Z.
- 21M.2.HL.TZ2.8c.i: using a light source with a smaller wavelength.
-
21M.2.HL.TZ2.8a.iii:
The separation of adjacent slits is d. Show that for the second-order diffraction maximum .
- 21M.2.HL.TZ2.8a.i: State the phase difference between the waves at V and Y.
- 21M.2.HL.TZ2.8c.ii: increasing the distance between the diffraction grating and the screen.
-
19N.2.HL.TZ0.10b(ii):
calculate the smallest value of d that will result in destructive interference between ray X and ray Y.
-
17N.2.HL.TZ0.6a.ii:
The distance from the centre of the pattern to A is 4.1 x 10–2 m. The distance from the screen to the slits is 7.0 m.
Calculate the width of each slit.
-
19M.2.HL.TZ2.3ei:
Calculate the frequency heard by the observer.
- 19M.2.HL.TZ2.8a: Deduce, in W m-2, the intensity at M.
- 17M.1.HL.TZ2.27: Blue light is incident on two narrow slits. Constructive interference takes place along...
-
18M.2.HL.TZ2.5b:
Monochromatic light from a single source is incident on two thin, parallel slits.
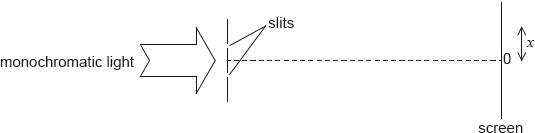
The following data are available.
The intensity I of light at the screen from each slit separately is I0. Sketch, on the axes, a graph to show the variation with distance x on the screen of the intensity of light on the screen for this arrangement.
-
18M.1.HL.TZ2.26:
A beam of monochromatic light is incident on a diffraction grating of N lines per unit length. The angle between the first orders is θ1.
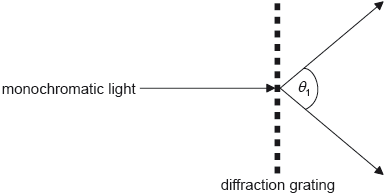
What is the wavelength of the light?
A.
B. N sin θ1
C. N sin
D.
-
18M.2.HL.TZ1.3b.ii:
Deduce, in mm, the width of one slit.
-
21M.2.HL.TZ2.8b:
Monochromatic light of wavelength 633 nm is normally incident on a diffraction grating. The diffraction maxima incident on a screen are detected and their angle θ to the central beam is determined. The graph shows the variation of sinθ with the order n of the maximum. The central order corresponds to n = 0.
Determine a mean value for the number of slits per millimetre of the grating.
- 21N.2.HL.TZ0.8d.i: State what will happen to the angular position of the primary maxima.

