| Date | November 2014 | Marks available | 5 | Reference code | 14N.1.hl.TZ0.12 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Prove that | Question number | 12 | Adapted from | N/A |
Question
The position vectors of the points \(A\), \(B\) and \(C\) are \(a\), \(b\) and \(c\) respectively, relative to an origin \(O\). The following diagram shows the triangle \(ABC\) and points \(M\), \(R\), \(S\) and \(T\).
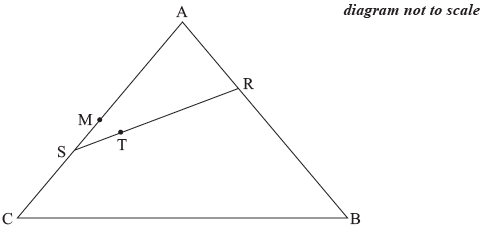
\(M\) is the midpoint of [\(AC\)].
\(R\) is a point on [\(AB\)] such that \(\overrightarrow {{\text{AR}}} = \frac{1}{3}\overrightarrow {{\text{AB}}} \).
\(S\) is a point on [\(AC\)] such that \(\overrightarrow {{\text{AS}}} = \frac{2}{3}\overrightarrow {{\text{AC}}} \).
\(T\) is a point on [\(RS\)] such that \(\overrightarrow {{\text{RT}}} = \frac{2}{3}\overrightarrow {{\text{RS}}} \).
(i) Express \(\overrightarrow {{\text{AM}}} \) in terms of \(a\) and \(c\).
(ii) Hence show that \(\overrightarrow {{\text{BM}}} = \frac{1}{2}\)\(a\) – \(b\)\( + \frac{1}{2}c\).
(i) Express \(\overrightarrow {{\text{RA}}} \) in terms of \(a\) and \(b\).
(ii) Show that \(\overrightarrow {RT} = - \frac{2}{9}a - \frac{2}{9}b + \frac{4}{9}c\).
Prove that \(T\) lies on [\(BM\)].
Markscheme
(i) \(\overrightarrow {{\text{AM}}} = \frac{1}{2}\overrightarrow {{\text{AC}}} \) (M1)
\( = \frac{1}{2}\)(\(c\) – \(a\)) A1
(ii) \(\overrightarrow {{\text{BM}}} = \overrightarrow {{\text{BA}}} + \overrightarrow {{\text{AM}}} \) M1
\( = a - b + \frac{1}{2}\)\((c - a)\) A1
\(\overrightarrow {{\text{BM}}} = \frac{1}{2}a - b + \frac{1}{2}c\) AG
[4 marks]
(i) \(\overrightarrow {{\text{RA}}} = \frac{1}{3}\overrightarrow {{\text{BA}}} \)
\( = \frac{1}{3}\)(a – b) A1
(ii) \(\overrightarrow {{\text{RT}}} = \frac{2}{3}\overrightarrow {{\text{RS}}} \)
\( = \frac{2}{3}\left( {\overrightarrow {{\text{RA}}} + \overrightarrow {{\text{AS}}} } \right)\) (M1)
\( = \frac{2}{3}\left( {\frac{1}{3}(a - b) + \frac{2}{3}(c - a)} \right)\;\;\;\)or equivalent. A1A1
\( = \frac{2}{9}\)\(\left( {a - b} \right)\) \( + \frac{4}{9}\)\(\left( {c - a} \right)\) A1
\(\overrightarrow {{\text{RT}}} = - \frac{2}{9}\)\(a\) – \( - \frac{2}{9}\)\(b\) \( + \frac{4}{9}\)\(c\) AG
[5 marks]
\(\overrightarrow {{\text{BT}}} = \overrightarrow {{\text{BR}}} + \overrightarrow {{\text{RT}}} \)
\( = \frac{2}{3}\overrightarrow {{\text{BA}}} + \overrightarrow {{\text{RT}}} \) (M1)
\( = \frac{2}{3}a - \frac{2}{3}b - \frac{2}{9}a - \frac{2}{9}b + \frac{4}{9}c\) A1
\(\overrightarrow {{\text{BT}}} = \frac{8}{9}\left( {\frac{1}{2}a - b + \frac{1}{2}c} \right)\) A1
point \(B\) is common to \(\overrightarrow {{\text{BT}}} \) and \(\overrightarrow {{\text{BM}}} \) and \(\overrightarrow {{\text{BT}}} = \frac{8}{9}\overrightarrow {{\text{BM}}} \) R1R1
so \(T\) lies on [\(BM\)] AG
[5 marks]
Total [14 marks]
Examiners report
A fairly straightforward question for candidates confident in the use of and correct notation for relative position vectors. Sign errors were the most common, but the majority of candidates did not gain all the reasoning marks for part (c). In particular, it was necessary to observe that not only were two vectors parallel, but that they had a point in common.
A fairly straightforward question for candidates confident in the use of and correct notation for relative position vectors. Sign errors were the most common, but the majority of candidates did not gain all the reasoning marks for part (c). In particular, it was necessary to observe that not only were two vectors parallel, but that they had a point in common.
A fairly straightforward question for candidates confident in the use of and correct notation for relative position vectors. Sign errors were the most common, but the majority of candidates did not gain all the reasoning marks for part (c). In particular, it was necessary to observe that not only were two vectors parallel, but that they had a point in common.

