| Date | November 2017 | Marks available | 2 | Reference code | 17N.3sp.hl.TZ0.1 |
| Level | HL only | Paper | Paper 3 Statistics and probability | Time zone | TZ0 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
A continuous random variable \(T\) has a probability density function defined by
\(f(t) = \left\{ {\begin{array}{*{20}{c}} {\frac{{t(4 - {t^2})}}{4}}&{0 \leqslant t \leqslant 2} \\ {0,}&{{\text{otherwise}}} \end{array}} \right.\).
Find the cumulative distribution function \(F(t)\), for \(0 \leqslant t \leqslant 2\).
Sketch the graph of \(F(t)\) for \(0 \leqslant t \leqslant 2\), clearly indicating the coordinates of the endpoints.
Given that \(P(T < a) = 0.75\), find the value of \(a\).
Markscheme
\(F(t) = \int_0^t {\left( {x - \frac{{{x^3}}}{4}} \right){\text{d}}x{\text{ }}\left( { = \int_0^t {\frac{{x(4 - {x^2})}}{4}{\text{d}}x} } \right)} \) M1
\( = \left[ {\frac{{{x^2}}}{2} - \frac{{{x^4}}}{{16}}} \right]_0^t{\text{ }}\left( { = \left[ {\frac{{{x^2}(8 - {x^2})}}{{16}}} \right]_0^t} \right){\text{ }}\left( { = \left[ {\frac{{ - 4 - {x^2}{)^2}}}{{16}}} \right]_0^t} \right)\) A1
\( = \frac{{{t^2}}}{2} - \frac{{{t^4}}}{{16}}{\text{ }}\left( { = \frac{{{t^2}(8 - {t^2})}}{{16}}} \right){\text{ }}\left( { = 1 - \frac{{{{(4 - {t^2})}^2}}}{{16}}} \right)\) A1
Note: Condone integration involving \(t\) only.
Note: Award M1A0A0 for integration without limits eg, \(\int {\frac{{t(4 - {t^2})}}{4}{\text{d}}t = \frac{{{t^2}}}{2} - \frac{{{t^4}}}{{16}}} \) or equivalent.
Note: But allow integration \( + \) \(C\) then showing \(C = 0\) or even integration without \(C\) if \(F(0) = 0\) or \(F(2) = 1\) is confirmed.
[3 marks]
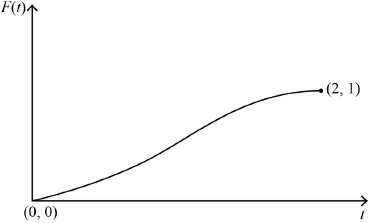
correct shape including correct concavity A1
clearly indicating starts at origin and ends at \((2,{\text{ }}1)\) A1
Note: Condone the absence of \((0,{\text{ }}0)\).
Note: Accept 2 on the \(x\)-axis and 1 on the \(y\)-axis correctly placed.
[2 marks]
attempt to solve \(\frac{{{a^2}}}{2} - \frac{{{a^4}}}{{16}} = 0.75\) (or equivalent) for \(a\) (M1)
\(a = 1.41{\text{ }}( = \sqrt 2 )\) A1
Note: Accept any answer that rounds to 1.4.
[2 marks]

